贵州省遵义市绥阳县2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2024-01-03 类型：期中考试

进入 出卷网 下载

一、选择题（本题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

  • 1. 在如图所示图形中，是中心对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 抛物线y＝3x2+2开口方向是（ ）
    A、向上 B、向下 C、向左 D、向右

    查看试题解析

  • 3. 如图，△ABC是⊙O的内接三角形，∠BAC＝35°，则∠BOC的度数为（   ）

    A、60° B、65° C、70° D、75°

    查看试题解析

  • 4. 方程（x+1）2＝0的根是（   ）
    A、x1＝x2＝1 B、x1＝x2＝﹣1 C、x1＝﹣1，x2＝1 D、无实根

    查看试题解析

  • 5. 抛物线y＝﹣（x﹣1）2+3的顶点坐标是（   ）
    A、（1，3） B、（﹣1，3） C、（﹣1，﹣3） D、（1，﹣3）

    查看试题解析

  • 6. 关于x的一元二次方程x2﹣2x﹣6＝0的根的情况是（   ）
    A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

    查看试题解析

  • 7. 用配方法解方程x2﹣4x+2＝0时，配方后所得的方程是（   ）
    A、（x﹣2）2＝2 B、（x+2）2＝2 C、（x﹣2）2＝1 D、（x﹣2）2＝﹣2

    查看试题解析

  • 8. 将二次函数y＝﹣3x2的图象平移后，得到二次函数y＝﹣3（x﹣1）2的图象，平移的方法可以是（   ）
    A、向左平移1个单位长度 B、向右平移1个单位长度 C、向上平移1个单位长度 D、向下平移1个单位长度

    查看试题解析

  • 9. 4月23日是世界读书日，据有关部门统计，某市2021年人均纸质阅读量约为4本，2023年人均纸质阅读量约为4.84本，设人均纸质阅读量年均增长率为x，则根据题意可列方程（   ）

    A、4（1+2x）＝4.84 B、4.84（1+x）2＝4 C、4（1+x）2＝4.84 D、4+4（1+x）+4（1+x）2＝4.84

    查看试题解析

  • 10. 已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，当y＜0时，x的取值范围是（   ）

    A、﹣1＜x＜2 B、x＞2 C、x＜﹣1 D、x＜﹣1或x＞2

    查看试题解析

  • 11. 如图，⊙O的半径为10，弦AB＝16，点M是弦AB上的动点且点M不与点A、B重合，若OM的长为整数，则这样的点M有几个？（   ）

    A、4 B、5 C、7 D、9

    查看试题解析

  • 12. 已知二次函数y＝x2+（1﹣m）x+1，当x＞1时，y随x的增大而增大，则m的取值范围是（   ）
    A、m＝﹣1 B、m＝3 C、m≤3 D、m＞﹣1

    查看试题解析

二、填空题（本题共4小题，每小题4分，共16分。答题请用0.5毫米黑色墨水的签字笔或钢笔直接答在答题卡的相应位置上。）

  • 13. 已知M（a，﹣3）和N（4，b）关于原点对称，则a+b＝ ．

    查看试题解析

  • 14. 在综合实践活动中，同学们借助如图所示的直角墙角（两边足够长），用24m长的篱笆围成一个矩形花园ABCD，则矩形花园ABCD的最大面积为m2.

    查看试题解析

  • 15. 关于x的一元二次方程（m﹣1）x2+x+m2﹣1＝0有一根为0，则m＝ ．

    查看试题解析

  • 16. 如图，在△ABC中，∠ACB＝90°，∠B＝30°，BC＝43 ， 点P是直角边BC上一动点（点P不与B，C重合），连接AP，将线段AP绕点A顺时针旋转60°得线段AD，连接CD，则线段CD的最小值是 ．

    查看试题解析

三、解答题（本题共9小题，共98分。答题请用0.5毫米黑色墨水的签字笔或钢笔书写在答题卡的相应位置上。答题时应写出必要的文字说明、证明过程或演算步骤。）

  • 17. 小明在学习配方法解一元二次方程后，用配方法解方程2x2﹣8x+3＝的过程如下．

    解：2x2﹣8x＝﹣3．①

    x2﹣4x＝﹣3．②

    x2﹣4x+4＝﹣3+4．③

    （x﹣2）2＝1．④

    x﹣2＝±1．⑤

    ∴x1＝3，x2＝1．⑥

    (1)、上述解方程的过程中，小明从第步开始出现了错误；（填序号）
    (2)、请利用配方法正确的解方程2x2﹣8x+3＝0．

    查看试题解析

  • 18. 如图，在平面直角坐标系xOy中，已知△ABC三个顶点的坐标分别为A（1，1），B（5，3），C（3，4）．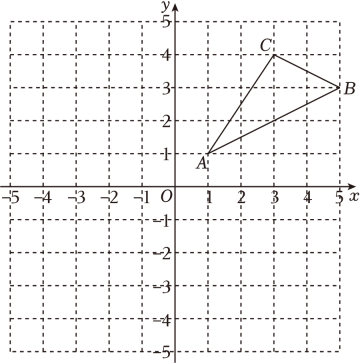

    (1)、画出△ABC关于原点O成中心对称的Δ A1B1C1；
    (2)、画出△ABC绕点O按逆时针方向旋转90°所得到的Δ A2B2C2；
    (3)、根据（1）（2）画出的图形，求出Δ AA1A2的面积．

    查看试题解析

  • 19. 已知关于x的一元二次方程x2+（m+2）x+m＝0．
    (1)、求证：无论m取何值，此方程总有两个不相等的实数根；
    (2)、若方程有两个实数根x1 ， x2 ， 且x1+x2+2x1x2＝1，求m的值．

    查看试题解析

  • 20. 石拱桥是我国古代人民勤劳和智慧的结晶（如图1），隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为AB⌢ ． 桥的跨度（弧所对的弦长）AB＝24m，设AB⌢所在圆的圆心为O，半径OC⊥AB，垂足为D．拱高（弧的中点到弦的距离）CD＝5m．连接OB．求这座石拱桥主桥拱的半径．（精确到1m）．

    查看试题解析

  • 21. 某商场销售一批儿童玩具，平均每天能售出20件，每件盈利40元．经调查发现：这种玩具的售价每降低1元，平均每天能多售出2件，设每件玩具降价x元．
    (1)、降价后，每件玩具的利润为元，平均每天的销售量为件；（用含x的式子表示）
    (2)、为了扩大销售，尽快减少库存，商场决定采取降价措施，但需要每天盈利1200元，那么每件玩具应降价多少元？

    查看试题解析

  • 22. 二次函数y＝ax2+bx+c中的x，y满足如表．

    x

    …

    ﹣1

    0

    1

    2

    …

    y

    …

    0

    ﹣3

    m

    ﹣3

    …

    (1)、求该抛物线的解析式；
    (2)、抛物线的顶点坐标为 ， 当x＞1时，y随x的增大而（填“增大”或“减小”）；
    (3)、直接写出当﹣1＜x＜2时，y的取值范围．

    查看试题解析

  • 23. 如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C，

    (1)、若∠ADE＝28°，求∠C的度数；
    (2)、若AC＝6，CE＝3，求⊙O半径的长．

    查看试题解析

  • 24. 有一个抛物线形的拱形桥洞，当桥洞的拱顶P（抛物线最高点）离水面的距离为4米时，水面的宽度OA为12米．现将它的截面图形放在如图所示的直角坐标系中．

    (1)、求这条抛物线的解析式．
    (2)、当洪水泛滥，水面上升，水面的宽度小于5米时，则必须马上采取紧急措施．某日涨水后，观察员测得桥洞的拱顶P到水面CD的距离只有1.5米，问：是否要采取紧急措施？并说明理由．

    查看试题解析

  • 25. 数学综合实践课上，同学们以“等腰三角形的旋转”为主题，开展如下探究活动：

    (1)、【操作探究】如图1，△ABC为等边三角形，将△ABC绕点A旋转180°，得到△ADE，连接BE，F是BE的中点，连接AF．

    ①写出图1中一个等于90°的角；

    ②图1中AF与DE的数量关系是 ．

    (2)、【迁移探究】如图2，将（1）中的等边△ABC绕点A逆时针旋转30°，得到△ADE，其他条件不变．探究AF与DE的数量关系，并说明理由．
    (3)、【拓展应用】如图3，在△ABC中，∠BAC＝90°，AB＝AC，BC＝22 ， 将△ABC绕点A旋转，得到△ADE，连接BE，F是BE的中点，连接AF．在旋转过程中，当∠EBC＝15°时，直接写出线段AF的长．

    查看试题解析