山东省济南市槐荫区2023-2024学年七年级上学期期中数学试卷
试卷更新日期:2024-01-03 类型:期中考试
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有
-
1. 如果“盈利3%”记作+3%,那么﹣5%表示( )A、少赚5% B、亏损﹣5% C、盈利5% D、亏损5%2. 下列几何体中,属于棱柱的是( )A、
 B、
B、 C、
C、 D、
D、 3. 据济南市统计局发布,2023年上半年蔬菜累计生产约3111000吨.数据3111000用科学记数法可表示为( )A、0.3111×106 B、3.111×106 C、3.111×107 D、31.11×1054. 下列各式符合代数式书写规范的是( )A、a9 B、x﹣3元 C、 D、5. 用一个平面去截一个正方体,不可能出现哪个截面?( )A、四边形 B、五边形 C、六边形 D、七边形6. 下列各组数中,相等的一组是( )A、﹣(﹣2)与﹣|﹣2| B、﹣32与(﹣3)2 C、﹣53与(﹣5)3 D、23与327. 已知|a+2|+|b﹣1|=0,则ab的值是( )A、2 B、1 C、﹣2 D、﹣18. 下列说法正确的有( )
3. 据济南市统计局发布,2023年上半年蔬菜累计生产约3111000吨.数据3111000用科学记数法可表示为( )A、0.3111×106 B、3.111×106 C、3.111×107 D、31.11×1054. 下列各式符合代数式书写规范的是( )A、a9 B、x﹣3元 C、 D、5. 用一个平面去截一个正方体,不可能出现哪个截面?( )A、四边形 B、五边形 C、六边形 D、七边形6. 下列各组数中,相等的一组是( )A、﹣(﹣2)与﹣|﹣2| B、﹣32与(﹣3)2 C、﹣53与(﹣5)3 D、23与327. 已知|a+2|+|b﹣1|=0,则ab的值是( )A、2 B、1 C、﹣2 D、﹣18. 下列说法正确的有( )①6x2﹣3x﹣2的项是6x2 , 3x,2;②一个多项式的次数是3,则这个多项式中只有一项的次数是3;③单项式﹣3πx2的系数是﹣3;④0是整式.
A、0个 B、1个 C、2个 D、3个9. 如图1,点A,B,C是数轴上从左到右排列的三个点,分别对应的数为﹣5,b,4,某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对齐刻度1.8cm,点C对齐刻度5.4cm.则数轴上点B所对应的数b为( ) A、﹣2 B、﹣3 C、﹣1 D、310. 如图所示的运算程序中,若开始输入的值为 , 我们发现第次输出的结果为 , 第次输出的结果为 , ……,则第2023次输出的结果为( )
A、﹣2 B、﹣3 C、﹣1 D、310. 如图所示的运算程序中,若开始输入的值为 , 我们发现第次输出的结果为 , 第次输出的结果为 , ……,则第2023次输出的结果为( )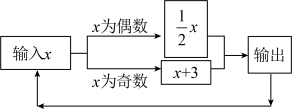 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6个小题.每小题4分,共24分.把答案填在答题卡的横线上.)
-
11. ﹣2023的相反数是 .12. 如图,下面的几何体是由图(填写序号)的平面图形绕直线旋转一周得到的.
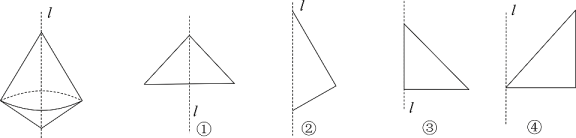 13. 某景点去年的游客数量为x人,今年的游客数量是去年的2倍还多470人,则今年的游客数量为 人.(用含x的代数式表示)14. 如果单项式2xm+2yn+3与x3y5是同类项,那么m+n= .15. 如图是一个正方体的展开图,则“数”字的对面的字是 .
13. 某景点去年的游客数量为x人,今年的游客数量是去年的2倍还多470人,则今年的游客数量为 人.(用含x的代数式表示)14. 如果单项式2xm+2yn+3与x3y5是同类项,那么m+n= .15. 如图是一个正方体的展开图,则“数”字的对面的字是 . 16. 定义一种新运算,规定:a⊕b=3a﹣b.若a⊕(﹣6b)=﹣2 , 请计算(2a+b)⊕(2a﹣5b)的值为 .
16. 定义一种新运算,规定:a⊕b=3a﹣b.若a⊕(﹣6b)=﹣2 , 请计算(2a+b)⊕(2a﹣5b)的值为 .三、解答题(本大题共10个小题,共86分.解答应写出文字说明,证明过程或演算步骤.)
-
17. 把下列各数在数轴上表示出来,并用“>”比较大小. , ﹣4.5,4, , ﹣1.
 18. 计算:(1)、3﹣(﹣7);(2)、﹣20+3+5﹣7.19. 计算:7a+3(a﹣3b)﹣2(b﹣3a)20. 由大小相同的小立方块搭成的几何体如图所示,请在方格中画出该几何体的主视图、俯视图和左视图.
18. 计算:(1)、3﹣(﹣7);(2)、﹣20+3+5﹣7.19. 计算:7a+3(a﹣3b)﹣2(b﹣3a)20. 由大小相同的小立方块搭成的几何体如图所示,请在方格中画出该几何体的主视图、俯视图和左视图. 21. 阅读下题解答:
21. 阅读下题解答:计算: .
分析:利用倒数的意义,先求出原式的倒数,再得原式的值.
解:×(﹣24)=﹣16+18﹣21=﹣19.
所以原式=﹣ .
根据阅读材料提供的方法,完成下面的计算: .
22. 某种T型零件尺寸如图所示(左右宽度相同),求: (1)、用含x,y的代数式表示阴影部分的周长.(2)、用含x,y的代数式表示阴影部分的面积.(3)、x=2,y=2.5时,计算阴影部分的面积.23. 某校举办了“废纸回收,变废为宝”活动,各班收集的废纸均以5kg为标准,超过的记为“+”,不足的记为“﹣”,七年级六个班级的废纸收集情况如表所示,统计员小虎不小心将一个数据弄脏看不清了,但他记得三班收集废纸最少,且收集废纸最多和最少的班级的质量差为4kg.
(1)、用含x,y的代数式表示阴影部分的周长.(2)、用含x,y的代数式表示阴影部分的面积.(3)、x=2,y=2.5时,计算阴影部分的面积.23. 某校举办了“废纸回收,变废为宝”活动,各班收集的废纸均以5kg为标准,超过的记为“+”,不足的记为“﹣”,七年级六个班级的废纸收集情况如表所示,统计员小虎不小心将一个数据弄脏看不清了,但他记得三班收集废纸最少,且收集废纸最多和最少的班级的质量差为4kg.班级
一
二
三
四
五
六
超过(不足)(kg)
+1
+2
﹣1.5
0
﹣1
 (1)、请你计算七年级六班同学收集废纸的质量;(2)、若本次活动收集废纸质量排名前三的班级可获得荣誉称号,请计算获得荣誉称号的班级收集废纸的总质量;(3)、若七年级六个班级将本次活动收集的废纸集中卖出,30kg(包括30kg)以内的2元/千克,超出30kg的部分2.5元/千克,求废纸卖出的总价格.24. 如图
(1)、请你计算七年级六班同学收集废纸的质量;(2)、若本次活动收集废纸质量排名前三的班级可获得荣誉称号,请计算获得荣誉称号的班级收集废纸的总质量;(3)、若七年级六个班级将本次活动收集的废纸集中卖出,30kg(包括30kg)以内的2元/千克,超出30kg的部分2.5元/千克,求废纸卖出的总价格.24. 如图 (1)、由图1得:2+4=2×3;由图2得:2+4+6=;由图3得:;(2)、则由图n可得:2+4+……+2(n+1)=;(3)、根据(2)的结论,求2+4+6+……+1000的值.25. 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,他从A处出发去看望B、C、D处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B{1,4},从B到A记为:B→A{﹣1,﹣4},其中第一个数表示左右方向,第二个数表示上下方向.
(1)、由图1得:2+4=2×3;由图2得:2+4+6=;由图3得:;(2)、则由图n可得:2+4+……+2(n+1)=;(3)、根据(2)的结论,求2+4+6+……+1000的值.25. 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,他从A处出发去看望B、C、D处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B{1,4},从B到A记为:B→A{﹣1,﹣4},其中第一个数表示左右方向,第二个数表示上下方向. (1)、图中A→C{ , },C→B{ , };(2)、若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的最短路程;(3)、若图中另有两个格点M、N,且M→A{1﹣a,b﹣5},M→N{5﹣a,b﹣2},则A→N应记为什么?直接写出你的答案.26. 综合探究
(1)、图中A→C{ , },C→B{ , };(2)、若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的最短路程;(3)、若图中另有两个格点M、N,且M→A{1﹣a,b﹣5},M→N{5﹣a,b﹣2},则A→N应记为什么?直接写出你的答案.26. 综合探究
【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现了许多重要的规律:如图1,若数轴上点A、点B表示的数分别为a、b(b>a),则线段AB的长(点A到点B的距离)可表示为b﹣a,请用上面材料中的知识解答下面的问题:
【问题情境】如图2,一个点从数轴上的原点开始,先向左移动2个单位长度到达点A,再向右移动3个单位长度到达点B,然后再向右移动5个单位长度到达点C.
(1)、【问题探究】请在图2中表示出A、B、C三点的位置;(2)、【问题探究】若点P从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,同时点M、N从点B、点C分别以每秒2个单位长度、每秒3个单位长度的速度沿数轴向右匀速运动.设运动时间为t秒(t>0).①点A到点B的距离AB= ▲ , 点A到点C的距离AC= ▲ ;
②用含t的代数式表示:t秒时,点P表示的数为 ▲ , 点M表示的数为 ▲ , 点N表示的数为 ▲ ;
③试探究在运动的过程中,3PN﹣4PM的值是否随着时间t的变化而变化?若变化,说明理由;若不变,请求其值.