四川省泸州市泸州七中2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2024-01-03 类型：期中考试

进入 出卷网 下载

一、选择题（本大题共12小题，每题3分，共36分．只有一项是符合题目要求的）．

  • 1. 下列运算正确的是（　　）
    A、x2+x3＝x5 B、x2•x3＝x6 C、x6÷x2＝x3 D、（3x3）2＝9x6

    查看试题解析

  • 2. 若某三角形两边的长分别是3和5，则此三角形第三边的长可能是（　　）
    A、2 B、3 C、8 D、1

    查看试题解析

  • 3. 王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（   ）

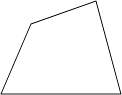    A、0根 B、1根 C、2根 D、3根

    查看试题解析

  • 4. 已知a﹣b＝3，ab＝2，则a2b﹣ab2的值为（　　）
    A、6 B、5 C、18 D、12

    查看试题解析

  • 5. 如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（   ）

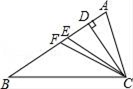    A、AB＝2BF B、∠ACE＝ 12 ∠ACB C、AE＝BE D、CD⊥BE

    查看试题解析

  • 6. 多项式a2﹣5a﹣6因式分解的结果是（　　）
    A、（a﹣2）（a+3） B、（a﹣6）（a+1） C、（a+6）（a﹣1） D、（a+2）（a﹣3）

    查看试题解析

  • 7. 如果一个多边形的内角和是外角和的3倍，那么这个多边形是
    A、四边形 B、六边形 C、八边形 D、十边形

    查看试题解析

  • 8. 如图，在△ABC和△ABD中，已知AC=AD ， 则添加以下条件，仍不能判定△ABC≌△ABD的是（    ）

    A、BC=BD B、∠ABC=∠ABD C、∠C=∠D=90° D、∠CAB=∠DAB

    查看试题解析

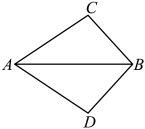  • 9. 如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AB，AC于点M，N，再分别以M，N为圆心，大于12MN的长为半径画弧，两弧交于点O，作射线AO交BC于点D．已知BD＝5，CD＝3，则点D到AB的距离为（　　）

    A、2 B、3 C、5 D、8

    查看试题解析

  • 10. 如图，在△ABC中，∠BCA＝40°，∠ABC＝60°．若BF是△ABC的高，与角平分线AE相交于点O，则∠EOF的度数为（　　）

    A、130° B、70° C、110 D、100°

    查看试题解析

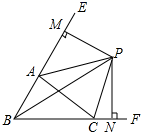
  • 11. 如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（  ）

    A、（a﹣b）2=a2﹣2ab+b2 B、（a+b）2=a2+2ab+b2 C、a2﹣b2=（a+b）（a﹣b） D、无法确定

    查看试题解析

  • 12. 如图，△ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的个数（   ）

    ①CP平分∠ACF；②∠ABC+2∠APC＝180°；③∠ACB＝2∠APB；④S△PAC＝S△MAP+S△NCP ．

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题（本大题共4小题，每小题3分，共12分）

  • 13. 分解因式：5x2﹣5y2＝ ．

    查看试题解析

  • 14. 如图，BC⊥AB，则图中阴影部分的面积为 ．

    查看试题解析

  • 15. 已知a+b=3，ab=﹣2，则a2+b2的值是 ．

    查看试题解析

  • 16. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图一）就是一例．这个三角形给出了（a+b）n（n＝1，2，3，4，5，6…）的展开式的系数规律．请你仔细观察下表中的规律，按照上述规律，则（a+b）6展开式中第二项的系数是 ；（a+b）98展开式中第三项的系数是  ．

    查看试题解析

三、（本大题共3小题，每题6分，共18分）

四、（本大题共2小题，每题7分，共14分）

  • 20. 先化简，再求值：[（a﹣2b）2﹣（a﹣2b）（a+2b）+4b2]÷2b，其中a＝1，b＝2．

    查看试题解析

  • 21. 已知：如图，AB∥DE，AC∥DF，BF＝EC.

    (1)、求证：△ABC≌△DEF；
    (2)、过点C作CG⊥AB于点G，若S△ABC＝9，DE＝6，求CG的长.

    查看试题解析

五、（本大题共2小题，题8分，共16分）

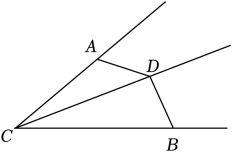
  • 22. 甲、乙两人共同计算一道整式乘法：（2x﹣a）（3x+b），由于甲抄错了第一个多项式中a的符号，得到的结果为6x2+11x﹣10；由于乙抄漏了第二个多项式中x的系数，得到的结果为2x2﹣9x+10．请你计算出a，b的值各是多少，并写出这道整式乘法的正确结果．

    查看试题解析

  • 23. 如图，AD＝BD，∠CAD+∠CBD＝180°，求证：CD平分∠ACB.

    查看试题解析

六、（本大题共2小题，24、25题各12分，共24分）

  • 24. 配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．我们定义：一个整数能表示成a2+b2（a、b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为5＝22+12 ， 所以5是“完美数”．
    (1)、【解决问题】：已知29是“完美数”，请将它写成a2+b2（a、b是整数）的形式．
    (2)、若x2﹣6x+5可配方成（x﹣m）2+n（m、n为常数），则mn＝ ．
    (3)、【探究问题】：已知x2+y2﹣2x+4y+5＝0，求x+y的值；
    (4)、已知S＝x2+4y2+4x﹣12y+k（xx、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．

    查看试题解析

  • 25. 在直角三角形ABC中，∠ACB＝90°，直线l过点C．

    (1)、当AC＝BC时，如图1，分别过点A和B作AD⊥直线l于点D，BE⊥直线l于点E．求证：DE＝AD+BE；
    (2)、当AC＝8cm，BC＝6cm时，如图2，BF⊥直线l于点K，且BK＝FK，连接CF．点M从A点出发，以每秒1cm的速度沿A→C路径运动，终点为C，点N以每秒3cm的速度沿F→C→B→C→F路径运动，终点为F，分别过点M、N作MD⊥直线l于点D，NE⊥直线l于点E，点M、N同时开始运动，各自达到相应的终点时停止运动，设运动时间为t秒．当△MDC与△CEN全等时，求t的值．

    查看试题解析