四川省广元市苍溪县2023-2024学年七年级上学期期中数学试卷

试卷更新日期：2024-01-03 类型：期中考试

进入出卷网下载

一、选择题（共10题，共30分）.

1. ﹣2的绝对值是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 计算5x²﹣3x²的结果是（　　）

A、2 B、2x² C、2x D、4x²

查看试题解析
3. 下列说法正确的是（　　）

A、2不是代数式 B、 $\frac{x + 1}{3}$ 是单项式 C、 $\frac{x - 3}{2}$ 的一次项系数是 1 D、1是单项式

查看试题解析
4. 已知a，b两数在数轴上对应的点如图所示，下列结论正确的是（　　）

A、a＜b B、ab＞0 C、a+b＜0 D、 $\frac{a}{b}$ ＞0

查看试题解析
5. 习近平总书记指出“善于学习，就是善于进步”．“国家中小学智慧云平台”上线的某天，全国大约有5450000人在平台上学习，将5450000这个数据用科学记数法表示为（　　）

A、545×10 B、0.545×10 C、5.45×10⁶ D、54.5×10⁵

查看试题解析
6. 下列各组的两个数中，运算后结果相等的是（）

A、﹣2⁴与（﹣2）⁴ B、5³与3⁵ C、﹣（﹣3）与﹣|﹣3| D、﹣1³与（﹣1）²⁰¹⁵

查看试题解析
7. 数轴上某一个点表示的数为 $a$ ，比 $a$ 小 $2$ 的数用 $b$ 表示，那么 $| a | + | b |$ 的最小值为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
8. 为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动．现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（　　）

A、8x元 B、10（100﹣x）元 C、8（100﹣x）元 D、（100﹣8x）元

查看试题解析
9. 如图所示的运算程序中，若开始输入的x值为15，则第1次输出的结果为18，第2次输出的结果为9，……，第2022次输出的结果为（　　）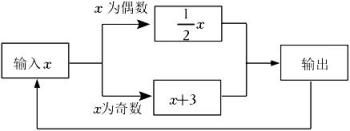

A、3 B、4 C、6 D、9

查看试题解析
10. 在求两位数的平方时，可以用“列竖式”的方法进行速算，求解过程如图所示．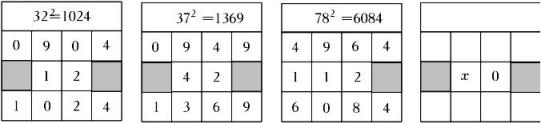
仿照前三个图，用“列竖式”的方法计算一个两位数的平方，部分过程如图所示，若这个两位数的个位数字为x，则这个两位数为（　　）（用含x的代数式表示）

A、11x B、x+50 C、﹣x+50 D、10x+5

查看试题解析

二、填空题（共6题；共24分）

11. 用四舍五入法取近似数，1.895精确到百分位后是．

查看试题解析
12. 若代数式﹣2x²y^m与 $\frac{3}{5} x^{n} y^{3}$ 是同类项，则代数式mⁿ＝．

查看试题解析
13. 若代数式﹣2x与代数式3x﹣1互为相反数，则x＝．

查看试题解析
14. 小明在计算多项式M加上x²﹣2x+9时，因误认为加上x²+2x+9，得到答案2x²+2x，则M应是．

查看试题解析
15. 计算 $(\frac{1}{3} + \frac{1}{4} + \frac{1}{5}) - 2 \times (\frac{1}{2} - \frac{1}{3} - \frac{1}{4} - \frac{1}{5}) - 3 \times (\frac{1}{3} + \frac{1}{4} + \frac{1}{5} - \frac{1}{6})$ 的结果是．

查看试题解析
16. 如图，在一组有规律的图案中，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，第3个图案由 $10$ 个基础图形组成，则第n（n是正整数）个图案由个基础图形组成．

查看试题解析

三、解答题（共96分）

17.

(1)、在数轴上表示下列各数，再用“＜”号把各数连接起来．
0，﹣（﹣1），﹣（+2），|﹣3|，﹣15，（﹣1）³ ．

(2)、求以上有理数的和．

查看试题解析
18. 计算：

(1)、（﹣2）³+（﹣3）×[（﹣4）²+2]﹣（﹣3）²÷（﹣2）；

(2)、 $\frac{11}{5} \times (\frac{1}{3} - \frac{1}{2}) \times \frac{3}{11} \div \frac{5}{4}$ ．

查看试题解析
19. 把下列各整式填入相应的圈里：
ab+c，2m，ax²+c，﹣ab²c，a，0，﹣ $\frac{1}{2}$ x，y+2．

查看试题解析
20. 化简求值：3a²b﹣2[2ab²﹣4（ab﹣ $\frac{3}{2}$ a²b）+ab]+（4ab²﹣a²b），其中a、b使得关于x的多项式2x³+（a+1）x²+（b﹣ $\frac{1}{2}$ ）x+3不含x²项和x项．

查看试题解析
21. 小刚在解数学题时，由于粗心把原题“两个代数式A和B，其中A＝？，B＝4x²﹣5x﹣6，试求A+B的值”中的“A+B”错误的看成“A﹣B”，结果求出的答案是﹣7x²+10x+12，请你帮他纠错，正确地算出A+B的值．

查看试题解析
22. 某检修小组乘一辆汽车沿公路检修线路，约定向东行驶为正，向西行驶为负，某天从A地出发到收工时，行程及方向记录如下．（长度单位：千米）
第一次
第二次
第三次
第四次
第五次
第六次
第七次
﹣4
+15
﹣2
+5
﹣1
+10
﹣3

(1)、收工时，检修小组在A地的什么位置？距A地多少千米？

(2)、若汽车每行驶1千米耗油0.5升，那么从出发到收工一共耗油多少升？

查看试题解析
23. 如图，一个长方形中剪下两个大小相同的正方形（有关线段的长如图所示），留下一个“T”型的图形（阴影部分）．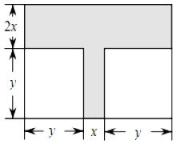

(1)、用含x，y的代数式表示“T”型图形的面积并化简；

(2)、若y＝3x＝15米，“T”型区域铺上价格为每平方米20元的草坪，请计算草坪的造价．

查看试题解析
24. 初一年级学生在5名教师的带领下去公园秋游，公园的门票为每人30元．现有两种优惠方案，甲方案：带队教师免费，学生按8折收费；乙方案：师生都7.5折收费．

(1)、若有m名学生，用代数式表示两种优惠方案各需多少元？

(2)、当m＝60时，采用哪种方案优惠？

(3)、当m＝105时，采用哪种方案优惠？

查看试题解析
25. 已知：A＝3a²﹣4ab，B＝a²+2ab.

(1)、求A﹣2B；

(2)、若|2a+1|+（2﹣b）²＝0，求A﹣2B的值.

查看试题解析
26. 如图所示，在数轴上点A、B、C表示的数分别为﹣2，1，6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC．

(1)、则AB＝， BC＝， AC＝；

(2)、点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B、点C分别以每秒2个单位长度和5单位长度的速度向右运动．请问：
①运动t秒后，点A与点B之间的距离AB为多少？（用含t的代数式表示）
②BC﹣AB的值是否随着运动时间t的变化而改变？若变化，请说明理由；若不变，请求其值；

(3)、由第（1）小题可以发现，AB+BC＝AC．若点C以每秒3个单位长度的速度向左运动，同时，点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动．请问：随着运动时间t的变化，AB，BC，AC之间是否存在类似于（1）的数量关系？请说明理由．

查看试题解析

第一次	第二次	第三次	第四次	第五次	第六次	第七次
﹣4	+15	﹣2	+5	﹣1	+10	﹣3