四川省广安市岳池县2023-2024学年八年级上学期期中数学试题

试卷更新日期：2024-01-03 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分.每小题只有一个选项符合题意，请将所选选项的代号填在对应题目的括号中）

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各组数，可以作为三角形的三边长的是（）

A、2，3，5 B、7，10，25 C、8，12，20 D、5，13，15

查看试题解析
3. 如图，△ABC中，∠ACB＝90°， D为BC上一点， DE⊥AB于点E，下列说法中错误的是（　　）

A、△ABC中，AC是BC上的高 B、△ABD中，DE是AB上的高 C、△ABD中，AC是BD上的高 D、△ADE中，AE是AD上的高

查看试题解析
4. 已知等腰三角形的一个外角等于100°，则它的顶角是( )

A、80° B、20° C、80°或20° D、不能确定

查看试题解析
5. 下列说法错误的是（）

A、有一个角是60°的等腰三角形是等边三角形 B、等腰三角形的角平分线、中线、高相互重合 C、如果一个三角形有两个角相等，那么这两个角所对的边相等 D、三个角都相等的三角形是等边三角形

查看试题解析
6. 如图，已知方格纸中是4个相同的正方形，则 $∠ 1 + ∠ 2 =$ （）

A、60° B、90° C、100° D、120°

查看试题解析
7. 如图，已知△ABC的三条边和三个角六个元素，则下面甲、乙、丙三个三角形中和△ABC不全等的图形是（）

A、只有甲 B、乙和丙 C、只有乙 D、只有丙

查看试题解析
8. 如图，已知AB＝AC ， ∠ADB＝∠E ，要使△BAD≌△CAE ，则不符合条件的是（）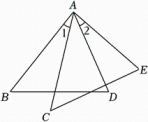

A、∠1＝∠2 B、∠B＝∠C C、BD＝CE D、∠BAD＝∠CAE

查看试题解析
9. 如图，点 $A$ ， $C$ ， $B$ 在同一直线上， $△ D A C$ 和 $△ E B C$ 均是等边三角形， $A E$ 与 $B D$ 交于点 $O$ ， $A E$ ， $B D$ 分别与 $C D$ ， $C E$ 交于点 $M$ ， $N$ ，有如下结论：
① $A E = B D$ ；② $△ A C M ≌ △ D C N$ ；③ $E M = B N$ ；④ $M N ∥ B C$ ；⑤ $∠ D O A = 60 °$ .其中正确的结论有：（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
10. 如图所示，在 $△ A B C$ 中，内角 $∠ B A C$ 与外角 $∠ C B E$ 的平分线相交于点 $P$ ， $B E = B C$ ， $P B$ 与 $C E$ 交于点 $H$ ， $P G ∥ A D$ 交 $B C$ 于 $F$ ，交 $A B$ 于 $G$ ，连接 $C P$ .下列结论：① $∠ A C B = 2 ∠ A P B$ ；② $S_{△ P A C} ： S_{△ P A B} = A C ： A B$ ；③ $C H = H E$ ；④ $∠ P C F = ∠ C P F$ ；⑤ $∠ C P A = ∠ C E A$ .其中，正确的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分.把正确答案填写在题中的横线上）

11. 如图，木工师傅做完窗框后，常象图中那样钉上一条斜拉的木条，这样做的数学原理是利用三角形的.

查看试题解析
12. 小明现在有两根 $5 c m$ ， $10 c m$ 的木棒，他想以这两根木棒为边做一个等腰三角形，还需再选一根cm长的木棒．

查看试题解析
13. 已知点 $P (a - 2 b ， - 2)$ 与点 $Q (- 6 ， 2 a + b)$ 关于原点对称，则 $a + b =$ .

查看试题解析
14. 一个正多边形的内角和为 $720 °$ ，则这个多边形的外角的度数为.

查看试题解析
15. 如图， $△ A B C$ 中， $D$ 点在 $B C$ 上，将 $D$ 点分别以 $A B$ 、 $A C$ 为对称轴，画出对称点 $E$ 、 $F$ .并连接 $A E$ 、 $A F$ .根据图中标示的角度，则 $∠ E A F$ 的度数为.

查看试题解析
16. 如图， $△ A B C$ 的面积为10， $D$ 、 $E$ 分别是 $A C$ ， $A B$ 上的点，且 $A D = C D$ ， $A E ： B E = 2 ： 1$ .连接 $B D$ ， $C E$ 交于点 $F$ ，连接 $A F$ 并延长交 $B C$ 于点 $H$ .则四边形 $B E F H$ 的面积为.

查看试题解析

三、解答题（本大题共8个小题，每小题6分，共48分.解答时应按要求写出该题解答的文字说明、证明过程或计算步骤）

17. 如图， $△ A B C$ 中， $∠ B = ∠ C$ ， $F D ⊥ B C$ ， $D E ⊥ A B$ ， $∠ A F D = 152 °$ ，求 $∠ E D F$ 的度数.

查看试题解析
18. 如图，在△ABC中，点D在边BC上，CD=AB，DE∥AB，∠DCE=∠A.求证：DE=BC.

查看试题解析
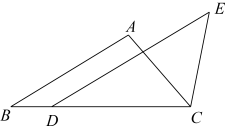19. 如图，由两根钢丝固定的高压电线杆，按要求当两根钢丝与电线杆的夹角相同时，固定效果最好.现已知钢丝触地点到电线杆的距离相等，即 $B O = C O$ ； $A O ⊥ B C$ ，那么请你判断图中两根钢丝的固定是否合乎要求，并说明理由.（电线杆的粗细忽略不计）

查看试题解析
20. 如图，在五边形 $A B C D E$ 中， $∠ A + ∠ B + ∠ E = 300 °$ ， $D P$ ， $C P$ 分别平分 $∠ E D C$ ， $∠ B C D$ ，求 $∠ P$ 的度数．

查看试题解析
21. 如图所示，已知四边形 $A B D C$ ，求证 $∠ B D C = ∠ A + ∠ B + ∠ C$ .

查看试题解析
22. 如图， $△ A B C$ 的三个顶点的坐标分别为 $A (- 2 ， 3)$ ， $B (1 ， 0)$ ， $C (2 ， 2)$ .
⑴作出 $△ A B C$ 关于 $y$ 轴对称的图形 $△ A_{1} B_{1} C_{1}$ ，并直接写出点 $A_{1}$ 的坐标；
⑵在 $x$ 轴上找一点 $P$ ，使得 $P A + P C$ 的值最小，请在图中作出点 $P$ .

查看试题解析
23. 中国棋盘中蕴含着平面直角坐标系，如图所示是中国象棋棋盘的一半，棋子“马”走的规则是沿“日”形对角线走.例如：图中“马”所在位置可以直接走到点 $A$ 、 $B$ 处.

(1)、如果“相”位于点 $(4 ， 2)$ ， “帅”位于点 $(0 ， 0)$ ，则“马”所在点的坐标为，点 $D$ 的坐标为.

(2)、若“马”的位置在 $C$ 点，为了到达“ $D$ ”点，请按“马”走的规则，写出一种你认为合理的行走路线，（在上图中标出行走路线即可）.

查看试题解析
24. 如图，点C在 $B D$ 上， $A B ⊥ B D ， E D ⊥ B D ， A C ⊥ C E ， A B = C D$ .求证： $△ A B C ≌ △ C D E$ .

查看试题解析

四、拓展探索题（本大题共2小题，每小题12分，共24分.解答时应按要求写出该题解答的文字说明、证明过程或计算步骤）

25. 如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD.

(1)、求证：△BCE≌△DCF；

(2)、求证：AB+AD=2AE.

查看试题解析
26. 如图，在等边 $△ A B C$ 中， $A B = 15 c m$ ， $D C = 7 c m$ .点 $M$ 以 $2 c m / s$ 的速度在线段 $C B$ 上由点 $C$ 向点 $B$ 运动，点 $N$ 在线段 $B A$ 上由 $B$ 点向 $A$ 点运动.设运动时间为 $t$ （秒）.

(1)、如果它们同时出发，点 $N$ 的运动速度与点 $M$ 的运动速度相等.
①经过多少秒， $△ B M N$ 和 $△ C D M$ 全等？
②经过多少秒， $△ B M N$ 是一个直角三角形？

(2)、设点 $N$ 的运动速度为 $x c m / s$ ，点 $N$ ，点 $M$ 同时出发，若 $△ B M N$ 和 $△ C D M$ 全等，求 $x$ ， $t$ 的值.

查看试题解析