四川省泸州市合江县2023-2024学年九年级上学期期中数学试卷
试卷更新日期:2024-01-03 类型:期中考试
一、选择题(本大题共12个小题,每小题3分,共36分)
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、矩形 B、平行四边形 C、等边三角形 D、等腰三角形2. 将一元二次方程化成一般形式,正确的是( )A、 B、 C、 D、3. 把抛物线向右平移3个单位,再向下平移2个单位,得到抛物线( )A、 B、 C、 D、4. 已知的半径为5,点P到圆心O的距离为 , 则点P在( )A、圆外 B、圆上 C、圆内 D、不能确定5. 关于二次函数的图象,下列叙述正确的是( )A、图象开口向下 B、图象的对称轴为直线 C、当时y随x增大而减小 D、图象经过点6. 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD,CB,AC,∠DOB=60°,EB=2,那么CD的长为( )
 A、 B、 C、 D、7. 二次函数的图象可能是( )A、
A、 B、 C、 D、7. 二次函数的图象可能是( )A、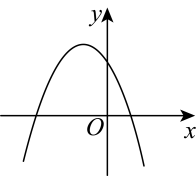 B、
B、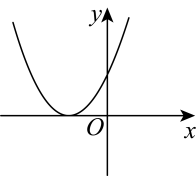 C、
C、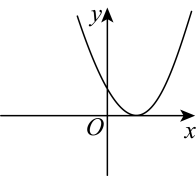 D、
D、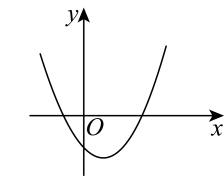 8. 在圆内接正六边形中,正六边形的边长为 , 则这个正六边形的中心角和边心距分别是( )A、 , B、 , C、 , D、 ,9. 我国南宋数学家杨辉在1275年提出的一个问题:“直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.”意思是:长方形的面积是864平方步,宽比长少12步,问宽和长各是几步.设宽为x步,根据题意列方程正确的是( )A、 B、 C、 D、10. 如图,已知圆锥侧面展开图的扇形面积为 , 扇形的弧长为 , 则圆锥的高是( )
8. 在圆内接正六边形中,正六边形的边长为 , 则这个正六边形的中心角和边心距分别是( )A、 , B、 , C、 , D、 ,9. 我国南宋数学家杨辉在1275年提出的一个问题:“直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.”意思是:长方形的面积是864平方步,宽比长少12步,问宽和长各是几步.设宽为x步,根据题意列方程正确的是( )A、 B、 C、 D、10. 如图,已知圆锥侧面展开图的扇形面积为 , 扇形的弧长为 , 则圆锥的高是( ) A、 B、 C、 D、11. 如图,在平面直角坐标系中,边长为2的正六边形的中心与原点O重台,轴,交y轴于点P.将绕点O逆时针旋转,每次旋转 , 则第2023次旋转结束时,点A的坐标为( )
A、 B、 C、 D、11. 如图,在平面直角坐标系中,边长为2的正六边形的中心与原点O重台,轴,交y轴于点P.将绕点O逆时针旋转,每次旋转 , 则第2023次旋转结束时,点A的坐标为( ) A、 B、 C、 D、12. 如图,抛物线(a,b,c为常数,且)关于直线对称,与x轴的其中一个交点坐标为 , 下列结论中:①;②关于x的一元二次方程的解是;③;④ , 其中正确的个数是( )
A、 B、 C、 D、12. 如图,抛物线(a,b,c为常数,且)关于直线对称,与x轴的其中一个交点坐标为 , 下列结论中:①;②关于x的一元二次方程的解是;③;④ , 其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本大题共4个小题,每小题3分,共12分)
-
13. 在平面直角坐标系中,点关于原点对称的点为 , 则 .14. 函数的图象如图所示,根据其中提供的信息,可求得方程的解是 .
 15. 已知x1 , x2是关于x的一元二次方程的两实数根,且 , 则m的值是 .16. 如图,半圆的直径AB=4,C,D是半圆的三等分点,则弦 , 与弧围成的阴影部分的面积是 .
15. 已知x1 , x2是关于x的一元二次方程的两实数根,且 , 则m的值是 .16. 如图,半圆的直径AB=4,C,D是半圆的三等分点,则弦 , 与弧围成的阴影部分的面积是 .
三、解答题(本大题共3个小题,每小题6分,共18分)
-
17. 解方程:18. 若函数是以x为自变量的二次函数.(1)、求k的值;(2)、当函数值时,求自变量x的值.19. 点A,B,C都在⊙O上,且 , 若 , 的半径为5,连接CO,求的长.

四、解答题(本大题共2个小题,每小题7分,共14分)
-
20. 如图,方格纸中的每个小正方形都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
 (1)、画出△ABC关于点P成中心对称的;(2)、画出△ABC绕点P逆时针方向旋转后所得到的 , 此时点的坐标为 .21. 若关于的一元二次方程 .(1)、若方程有两个实数根,求m的范围;(2)、若方程的一个根是 , 求另一个根及值.
(1)、画出△ABC关于点P成中心对称的;(2)、画出△ABC绕点P逆时针方向旋转后所得到的 , 此时点的坐标为 .21. 若关于的一元二次方程 .(1)、若方程有两个实数根,求m的范围;(2)、若方程的一个根是 , 求另一个根及值.五、解答题(本大题共2个小题,每小题8分,共16分)
-
22. 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上,球飞行的路线看做抛物线),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M处,距地面4米高,之后球在C点落地.
 (1)、当足球开始飞出到第一次落地时,求足球飞行线路所在抛物线的解析式;(2)、求足球第一次落地点C距守门员多少米?(用根号表示)23. 超市以每件25元的进价购进一批商品,当商品售价为40元时,三月份销售256件,四、五月该商品十分畅销,销售量持续上涨,在售价不变的基础上,五月份的销售量达到400件.(1)、求四、五这两个月销售量的月平均增长百分率.(2)、经市场预测,六月份的销售量将与五月份持平,现商场为了减少库存,采用降价促销方式,经调查发现,该商品每降价1元,月销量增加5件,当商品降价多少元时,商场六月份可获利4250元?
(1)、当足球开始飞出到第一次落地时,求足球飞行线路所在抛物线的解析式;(2)、求足球第一次落地点C距守门员多少米?(用根号表示)23. 超市以每件25元的进价购进一批商品,当商品售价为40元时,三月份销售256件,四、五月该商品十分畅销,销售量持续上涨,在售价不变的基础上,五月份的销售量达到400件.(1)、求四、五这两个月销售量的月平均增长百分率.(2)、经市场预测,六月份的销售量将与五月份持平,现商场为了减少库存,采用降价促销方式,经调查发现,该商品每降价1元,月销量增加5件,当商品降价多少元时,商场六月份可获利4250元?六、解答题(本大题共2个小题,每小题12分,共24分)

