贵州省六盘水市2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-03 类型:期中考试
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
-
1. 下列各数中,是无理数的是( )A、-2 B、1.414 C、 D、2. 下列函数中是一次函数的是( )A、 B、 C、 D、3. 如图,小明从点出发,先向西走 , 再向南走到达点 , 如果点的位置用表示,那么表示的位置是( )
 A、点A B、点B C、点C D、点D4. 下列各组数据为勾股数的是( )A、7,24,25 B、2,3,4 C、 , , D、1, ,5. 若点在一次函数的图象上,则点一定不在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限6. 在中,斜边 , 则的值为( )A、15 B、25 C、50 D、无法计算7. 下列说法正确的是( )A、一定是非负数 B、立方根等于它本身的数是-1和1 C、的平方根是 D、81算术平方根是-98. 已知点和点在直线上,则( )A、 B、 C、 D、无法判定9. 若直角三角形的三边长分别为、、 , 其中 , , 则的值为( )A、15 B、225 C、63 D、225或6310. 实数、在数轴上的位置如图所示,则下列结论正确的是( )
A、点A B、点B C、点C D、点D4. 下列各组数据为勾股数的是( )A、7,24,25 B、2,3,4 C、 , , D、1, ,5. 若点在一次函数的图象上,则点一定不在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限6. 在中,斜边 , 则的值为( )A、15 B、25 C、50 D、无法计算7. 下列说法正确的是( )A、一定是非负数 B、立方根等于它本身的数是-1和1 C、的平方根是 D、81算术平方根是-98. 已知点和点在直线上,则( )A、 B、 C、 D、无法判定9. 若直角三角形的三边长分别为、、 , 其中 , , 则的值为( )A、15 B、225 C、63 D、225或6310. 实数、在数轴上的位置如图所示,则下列结论正确的是( ) A、 B、 C、 D、11. 已知 , 分别是的整数部分和小数部分,那么的值是( )A、 B、 C、 D、12. 如图,直线与轴交于点 , 与直线交于点 , 则关于的一元一次方程的解为( )
A、 B、 C、 D、11. 已知 , 分别是的整数部分和小数部分,那么的值是( )A、 B、 C、 D、12. 如图,直线与轴交于点 , 与直线交于点 , 则关于的一元一次方程的解为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:每小题4分,共16分.
-
13. 的算术平方根的相反数是 .14. 已知直线经过原点和 , 那么它的函数表达式为 .15. 若实数 , 满足 , 则的值为 .16. 如图,在中, , 于点D.为线段上一点,连结 , 将边沿折叠,使点的对称点落在的延长线上.若 , , 则的面积为 .

三、解答题:本大题9小题,共98分.解答时应写出必要的文字说明、证明过程或演算步骤.
-
17.(1)、;(2)、 .18. 已知 , , , .(1)、请化简这四个数.(2)、根据化简结果,列式表示这四个数中“有理数的和”与“无理数的积”的差,然后计算结果.19. 已知:5是的平方根,的立方根是3.(1)、求 , 的值;(2)、求出的平方根.20. 图①是某品牌婴儿车,图②为其简化结构示意图,根据安全标准需满足 , 现测得 , , , 其中与之间由一个固定为的零件连接(即 , 通过计算说明该车是否符合安全标准.
图①
 图②
图② 21. 如图,在平面直角坐标系网格中,三角形的顶点坐标分别是 , , . 将三角形平移,使顶点平移到坐标原点处,得到三角形 .
21. 如图,在平面直角坐标系网格中,三角形的顶点坐标分别是 , , . 将三角形平移,使顶点平移到坐标原点处,得到三角形 . (1)、点的坐标是 , 点的坐标是 .(2)、画出平移后的 .(3)、求的面积.22. 《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺)将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索的长度.
(1)、点的坐标是 , 点的坐标是 .(2)、画出平移后的 .(3)、求的面积.22. 《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺)将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索的长度.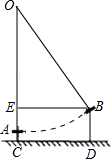 23. 如图,在平面直角坐标系中,直线与轴交于点 , 且点 , .
23. 如图,在平面直角坐标系中,直线与轴交于点 , 且点 , .
求:
(1)、 , 的值和点的坐标;(2)、的面积.24. 某城市出租车的收费标准为:千米以内(含千米)收费元,超过千米时,超过部分每千米收费元.(1)、写出车费(元)和行车里程(千米)之间的关系式;(2)、甲乘坐千米需付多少元钱?25. 综合与探究:如图①,平面直角坐标系中,一次函数的图象分别与轴轴交于点 , , 点是线段的中点,点与点关于轴对称,作直线 .图①
 图②
图② 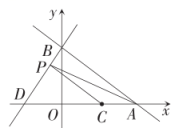 图③
图③ (1)、求 , 两点的坐标;(2)、求直线的函数表达式;(3)、若点是直线上的一个动点.
(1)、求 , 两点的坐标;(2)、求直线的函数表达式;(3)、若点是直线上的一个动点.请从 , 两题中任选一题作答.我选择 ▲ 题.
A.如图②,连接 , . 求为直角三角形时点的坐标.
B.如图③,连接 , 过点作轴于点 . 求为等腰直角三角形时点的坐标.