贵州省六盘水市2023-2024学年七年级上学期期中数学试题
试卷更新日期:2024-01-03 类型:期中考试
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
-
1. 若向东走25m,记为 , 则向西走15m记为( )A、 B、 C、 D、2. 下列各整式中,次数为4次的单项式是( )A、 B、 C、 D、3. 下图是由6个完全相同的正方体组成的立体图形,它的俯视图是( )
 A、
A、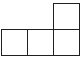 B、
B、 C、
C、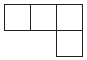 D、
D、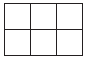 4. 如果a的相反数是 , 那么a的倒数是( )A、 B、 C、 D、5. 下列运算中,结果最小的是( )A、 B、 C、 D、6. 若单项式与单项式是同类项,则的值是( )A、2 B、3 C、4 D、57. 下列各式计算中,正确的是( )A、 B、 C、 D、8. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,则该正方体与“努”相对面上的汉字是( )
4. 如果a的相反数是 , 那么a的倒数是( )A、 B、 C、 D、5. 下列运算中,结果最小的是( )A、 B、 C、 D、6. 若单项式与单项式是同类项,则的值是( )A、2 B、3 C、4 D、57. 下列各式计算中,正确的是( )A、 B、 C、 D、8. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,则该正方体与“努”相对面上的汉字是( ) A、我 B、力 C、学 D、习9. 关于多项式的描述正确的是( )A、常数项是1 B、一次项是xy C、二次项是 D、三次项是10. 已知 , 则代数式的值为( )A、5 B、 C、 D、811. 点A,B分别对应数a,b,它们在数轴上的位置如图,则( )
A、我 B、力 C、学 D、习9. 关于多项式的描述正确的是( )A、常数项是1 B、一次项是xy C、二次项是 D、三次项是10. 已知 , 则代数式的值为( )A、5 B、 C、 D、811. 点A,B分别对应数a,b,它们在数轴上的位置如图,则( ) A、 B、 C、 D、12. 观察下列等式;;;;;;;…,通过观察,用你所发现的规律确定的个位数字是( )A、6 B、4 C、8 D、2
A、 B、 C、 D、12. 观察下列等式;;;;;;;…,通过观察,用你所发现的规律确定的个位数字是( )A、6 B、4 C、8 D、2二、填空题:每小题4分,共16分.
-
13. 2023年10月1日清晨,30.2万名民众齐聚天安门广场观看升旗仪式,庆祝中华人民共和国成立74周年.将302000这个数用科学记数法可表示为 , 则n的值是 .14. 单项式的系数是 .15. 如图所示的运算程序中,若开始输入的x值为50,我们发现第1次输出的结果为25,第2次给出的结果为32,…,则第2023次输出的结果是 .
 16. 已知整数、、、、…满足下列条件: , , , , …,(n为正整数)依此类推,则的值为 .
16. 已知整数、、、、…满足下列条件: , , , , …,(n为正整数)依此类推,则的值为 .三、解答题:本大题9小题,共98分.解答时应写出必要的文字说明、证明过程或演算步骤.
-
17. 计算:(1)、(2)、18. 已知,如图是由几个小正方体所组成几何体的从上面看到的几何体的形状图,小正方体中的数字表示在该位置的小正方体的个数,请分别画出这个几何体的从正面、左面看到的几何体的形状图.
 19. 在数轴上画出表示下列各数的点,并将这些数按照从小到大的顺序用“”号连接起来:、、0、、 .
19. 在数轴上画出表示下列各数的点,并将这些数按照从小到大的顺序用“”号连接起来:、、0、、 . 20. 已知:长为的铝条,裁下一部分后可以围成一个长方形铝框(部分数据如下图所示)
20. 已知:长为的铝条,裁下一部分后可以围成一个长方形铝框(部分数据如下图所示)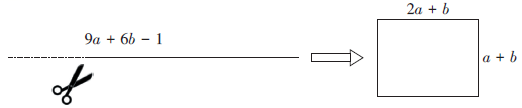 (1)、求裁下的铝条的长;(2)、若裁下的铝条的长为30cm,求长方形铝框的周长.21. 已知 .(1)、化简A;(2)、若 , 且A与B的差不含x的一次项,求a的值.22. 一名快递员每天在一条南北走向的公路上送快递,以物流公司为原点,向南走记为正,向北走记为负,这名快递员某一天的具体行程如下:(单位:千米)
(1)、求裁下的铝条的长;(2)、若裁下的铝条的长为30cm,求长方形铝框的周长.21. 已知 .(1)、化简A;(2)、若 , 且A与B的差不含x的一次项,求a的值.22. 一名快递员每天在一条南北走向的公路上送快递,以物流公司为原点,向南走记为正,向北走记为负,这名快递员某一天的具体行程如下:(单位:千米), , , , , .
(1)、这个快递员走完以上行程后在物流公司的什么位置?(2)、如果快递员所开的车100千米耗油5升,那么他走完以上行程耗油多少升?23. 做大小两个长方体纸盒,尺寸如下(单位:cm):长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)、1个小纸盒的表面积是cm2 , 1个大纸盒的表面积是cm2(用含a,b,c的式子表示);(2)、求做这样的2个小纸盒和1个大纸盒共用料多少平方厘米?(用含a,b,c的式子表示)(3)、求做这样的1个大纸盒比做这样的1个小纸盒多用料多少平方厘米?(用含a,b,c的式子表示)24. 探究与发现观察下列等式的规律,解答下列问题;
, , , , , …
(1)、第6个等式为 , 第100个等式;(2)、第n个等式为(用含n的代数式表示,n为正整数);(3)、设 , , , …, . 求:的值.25. 结合数轴与绝对值的知识回答下列问题: (1)、数轴上表示2和5两点之间的距离是;表示和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距高等于;(2)、如果 , 请计算x的值;(3)、若 , , 且数a、b在数轴上表示的数分别是点A、点B,求A、B两点之间的最大距离和最小距离.(4)、若数轴上表示数a的点位于与5之间,则的值是多少?
(1)、数轴上表示2和5两点之间的距离是;表示和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距高等于;(2)、如果 , 请计算x的值;(3)、若 , , 且数a、b在数轴上表示的数分别是点A、点B,求A、B两点之间的最大距离和最小距离.(4)、若数轴上表示数a的点位于与5之间,则的值是多少?