云南省昆明市安宁市昆钢一中2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2024-01-03 类型：期中考试
一、选择题（共12小题，每小题3分，共36分）
-
1. 自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中图案是轴对称图形的是（ ）A、
打喷嚏 捂口鼻
B、
喷嚏后 慎揉眼
C、
勤洗手 勤通风
D、
戴口罩 讲卫生
2. 下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（ ）A、3cm，4cm，8cm B、8cm，7cm，15cm C、13cm，12cm，20cm D、5cm，5cm，11cm3. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ）
A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点4. 下列条件中，不能判定直线MN是线段AB（M，N不在AB上）的垂直平分线的是（ ）A、MA=MB，NA=NB B、MA=MB，MN⊥AB C、MA=NA，MB=NB D、MA=MB，MN平分AB5. 如图，在△ABC中，D是BC延长线上一点，∠B＝30°，∠ACD＝110°，则∠A等于（ ）
A、60° B、70° C、80° D、90°6. 如图，AB＝DB，BC＝BE，欲证△ABE≌△DBC，则可增加的条件时（ ）
A、∠ABE＝∠DBE B、∠A＝∠D C、∠E＝∠C D、∠ABD＝∠EBC7. 等腰三角形的两边分别为12和6，则这个三角形的周长是（ ）A、24 B、18 C、30 D、24或308. 如图，若△ABC与△A′B′C′关于直线l对称，则下列结论不一定正确的是（ ）
A、∠BAC＝∠B′A′C′ B、△ABC≌△A′B′C′ C、直线l垂直平分 AA′ D、BB′＝2AA′9. 如图，等边△ABC的两条高AD和BE相交于点O，则∠DOE度数为（ ）
A、60° B、90° C、120° D、150°10. 如图 ，要测量河两岸相对的两点 A，B的距离，先在 AB的垂线 BF上取两点 C，D，使 BC＝CD，再作出 BF的垂线 DE，使点 A，C，E在同一条直线上（如图），可以说明△ABC≌△EDC，得 AB＝DE，因此测得 DE的 长就是 AB的长，判定△ABC≌△EDC，最恰当的理由是（ ）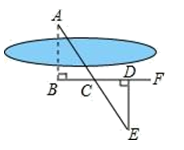
A、SAS B、HL C、SSS D、ASA11. 如图，已知方格纸中是4个相同的正方形，则∠1与∠2的和为（ ）
A、100° B、90° C、60° D、45°12. 如图，在Rt△ABC中，∠B＝90°，以点A为圆心，适当长为半径画弧，分别交AB、AC于点D，E，再分别以点D、E为圆心，大于DE为半径画弧，两弧交于点F，作射线AF交边BC于点G，若BG＝1，AC＝4，则△ACG的面积是（ ）
A、1 B、 C、2 D、二、填空题（共4小题，每小题2分，共8分）
-
13. 随着人们物质生活的提高，手机成为一种生活中不可缺少的东西，手机很方便携带，但唯一的缺点就是没有固定的支点．为了解决这一问题，某工厂研制生产了一种如图所示的手机支架．把手机放在上面就可以方便地使用手机，这是利用了三角形的 ．
14. 在平面直角坐标系中，点A的坐标是（2，﹣1），若点B与点A关于x轴对称，则点B的坐标是 ．15. 小林从P点向西直走8米后，向左转，转动的角度为α，再走8米，如此重复，小林共走了72米回到点P，则α为 ．16. 如图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A= ．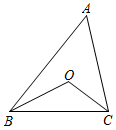
三、解答题（共8题，共56分）
-
17. 如图，AB=DE，AC=DF，BE=CF．求证：AC∥DF．
18. 一个多边形，它的内角和比外角和的4倍多180°，求这个多边形的边数及内角和度数．
19. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）点A，B，C的坐标分别为（2，4），（1，1），（3，2）．
(1)、请作出△ABC关于x轴对称的△A′B′C′，并写出A'，B'，C'的坐标．(2)、求△ABC的面积．(3)、在y轴上找一点P，使得AP+BP最小．20. 如图，在△ABC中，AB＝AC，∠B＝30°，D为BC边上一点，∠DAB＝45°.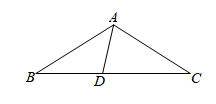
(1)、求∠DAC的度数；(2)、请说明：AB＝CD.21. 如图，已知：CD⊥AB于D，BE⊥AC于E，且BD＝CE，BE交CD于点O．求证：AO平分∠BAC．
