浙江省湖州市重点中学2023-2024学年高三上学期期中测试数学试卷
试卷更新日期:2024-01-02 类型:期中考试
一、单选题(1-8题为单选题,每小题只有一个正确选项,每小题5分,共40分)
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 已知非零向量 , , 满足 , , 若为在上的投影向量,则向量 , 夹角的余弦值为( )A、 B、 C、 D、3. 设(为虚数单位)为复数,则下列说法正确的是( )A、若是纯虚数,则或 B、复数模长的平方值等于复数的平方值 C、若的模长为 , 则的最大值为 D、若 , 则4. 若数列满足 , , 则满足不等式的最大正整数为( )A、28 B、29 C、30 D、315. 甲箱中有个红球,个白球和个黑球;乙箱中有个红球,个白球和个黑球.先从甲箱中随机取出一球放入乙箱中,分别以、、表示由甲箱中取出的是红球、白球和黑球的事件;再从乙箱中随机取出一球,以表示由乙箱中取出的球是红球的事件,则下列结论错误的是( )A、 B、 C、事件与事件不相互独立 D、、、两两互斥6. 设函数若恰有5个不同零点,则正实数的范围为( )A、 B、 C、 D、7. 对于平面上点和曲线 , 任取上一点 , 若线段的长度存在最小值,则称该值为点到曲线的距离,记作 . 下列结论中正确的个数为( )
①若曲线是一个点,则点集所表示的图形的面积为;②若曲线是一个半径为的圆,则点集所表示的图形的面积为;③若曲线是一个长度为的线段,则点集所表示的图形的面积为;④若曲线是边长为的等边三角形,则点集所表示的图形的面积为 .
A、1 B、2 C、3 D、48. 已知数列{an}满足 , 对于函数f(x)=x|x|,定义F(n)= .①若{an}为等比数列,则F(n)>0恒成立;②若{an}为等差数列,则F(n)>0恒成立.
关于上述命题,以下说法正确的是( )
A、①②都正确 B、①②都错误 C、①正确,②错误 D、①错误,②正确二、多选题(9-12题为多选题,每小题有2-4个正确选项,全部选对得5分,部分选对得2分,共20分)
-
9. 如图所示,棱长为3的正方体中,为线段上的动点(不含端点),则下列结论正确的是( )
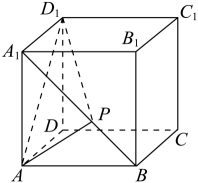 A、 B、与所成的角可能是 C、是定值 D、当时,点到平面的距离为110. 已知的内角所对的边分别为 , 下列四个命题中正确的是( )A、若 , 则一定是等腰三角形 B、若 , 则是等腰三角形 C、若 , 则一定是等边三角形 D、若 , 则是直角三角形11. 已知双曲线C:的左焦点为F,P为C右支上的动点,过P作C的一条渐近线的垂线,垂足为A,O为坐标原点,则下列说法正确的是( )A、点F到C的一条渐近线的距离为2 B、双曲线C的离心率为 C、则P到C的两条渐近线的距离之积大于4 D、当最小时,则的周长为12. 已知函数为定义在上的偶函数, , 且 , 则( )A、 B、的图象关于点对称 C、以6为周期的函数 D、
A、 B、与所成的角可能是 C、是定值 D、当时,点到平面的距离为110. 已知的内角所对的边分别为 , 下列四个命题中正确的是( )A、若 , 则一定是等腰三角形 B、若 , 则是等腰三角形 C、若 , 则一定是等边三角形 D、若 , 则是直角三角形11. 已知双曲线C:的左焦点为F,P为C右支上的动点,过P作C的一条渐近线的垂线,垂足为A,O为坐标原点,则下列说法正确的是( )A、点F到C的一条渐近线的距离为2 B、双曲线C的离心率为 C、则P到C的两条渐近线的距离之积大于4 D、当最小时,则的周长为12. 已知函数为定义在上的偶函数, , 且 , 则( )A、 B、的图象关于点对称 C、以6为周期的函数 D、三、填空题(13-16题为填空题,请在空白处填出正确答案,每小题5分,共20分)
-
13. 已知 , 若存在使得 , 则k的最大值为 .14. 已知空间一个平面与一个正方体的12条棱所成的角都等于 , 则=.15. 若平面上的三个单位向量、、满足 , , 则的所有可能的值组成的集合为 .16. 若存在实常数和 , 使得函数和对其公共定义域上的任意实数都满足和恒成立,则称直线为和的“隔离直线”.已知函数 , , , 则有下列命题:
①与有“隔离直线”;
②和之间存在“隔离直线”,且的最小值为;
③和之间存在“隔离直线”,且的取值范围是;
④和之间存在唯一的“隔离直线” .
其中真命题的序号为 . (请填上所有正确命题的序号)
四、解答题(17-22题为解答题,17题10分,18-22题每题12分,请在答题纸固定位置填入答案和解答步骤,共70分)
-
17. 2023年10月22日,汉江生态城2023襄阳马拉松在湖北省襄阳市成功举行,志愿者的服务工作是马拉松成功举办的重要保障,襄阳市新时代文明实践中心承办了志愿者选拔的面试工作.现随机抽取了100名候选者的面试成绩,并分成五组:第一组 , 第二组 , 第三组 , 第四组 , 第五组 , 绘制成如图所示的频率分布直方图.已知第一、二组的频率之和为0.3,第一组和第五组的频率相同.
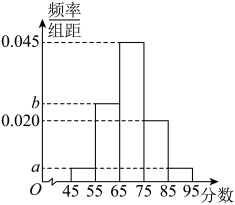 (1)、估计这100名候选者面试成绩的平均数和第25百分位数;(2)、现从以上各组中用分层随机抽样的方法选取20人,担任本市的宣传者.
(1)、估计这100名候选者面试成绩的平均数和第25百分位数;(2)、现从以上各组中用分层随机抽样的方法选取20人,担任本市的宣传者.若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为62和40,第四组面试者的面试成绩的平均数和方差分别为80和70,据此估计这次第二组和第四组面试者所有人的方差.
18. 已知四棱锥 , 底面为平行四边形, , , , .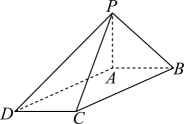 (1)、证明:平面;(2)、若 , 求二面角的正弦值.19. 在锐角中,设边所对的角分别为 , 且 .(1)、证明:(2)、若 , 求的取值范围.20. 已知椭圆的焦距为 , 离心率为 , 椭圆的左右焦点分别为、 , 直角坐标原点记为 . 设点 , 过点作倾斜角为锐角的直线与椭圆交于不同的两点、 .(1)、设椭圆上有一动点 , 求的取值范围;(2)、设线段的中点为 , 当时,判别椭圆上是否存在点 , 使得非零向量与向量平行,请说明理由.21. 已知空间向量列 , 如果对于任意的正整数 , 均有 , 则称此空间向量列为“等差向量列”,称为“公差向量”;空间向量列 , 如果且对于任意的正整数 , 均有 , , 则称此空间向量列为“等比向量列”,常数称为“公比”.(1)、若是“等差向量列”,“公差向量” , , ;是“等比向量列”,“公比” , , . 求 .(2)、若是“等差向量列”, , 记 , 且 , 等式对于和2均成立,且 , 求的最大值.22. 设是定义在上的函数,若存在区间和 , 使得在上严格减,在上严格增,则称为“含谷函数”,为“谷点”,称为的一个“含谷区间”.(1)、已知实数 , 是含谷函数,且是它的一个含谷区间,求的取值范围;(2)、设 , . 设函数是含谷函数,是它的一个含谷区间,并记的最大值为 . 若 , 且 , 求的最小值.
(1)、证明:平面;(2)、若 , 求二面角的正弦值.19. 在锐角中,设边所对的角分别为 , 且 .(1)、证明:(2)、若 , 求的取值范围.20. 已知椭圆的焦距为 , 离心率为 , 椭圆的左右焦点分别为、 , 直角坐标原点记为 . 设点 , 过点作倾斜角为锐角的直线与椭圆交于不同的两点、 .(1)、设椭圆上有一动点 , 求的取值范围;(2)、设线段的中点为 , 当时,判别椭圆上是否存在点 , 使得非零向量与向量平行,请说明理由.21. 已知空间向量列 , 如果对于任意的正整数 , 均有 , 则称此空间向量列为“等差向量列”,称为“公差向量”;空间向量列 , 如果且对于任意的正整数 , 均有 , , 则称此空间向量列为“等比向量列”,常数称为“公比”.(1)、若是“等差向量列”,“公差向量” , , ;是“等比向量列”,“公比” , , . 求 .(2)、若是“等差向量列”, , 记 , 且 , 等式对于和2均成立,且 , 求的最大值.22. 设是定义在上的函数,若存在区间和 , 使得在上严格减,在上严格增,则称为“含谷函数”,为“谷点”,称为的一个“含谷区间”.(1)、已知实数 , 是含谷函数,且是它的一个含谷区间,求的取值范围;(2)、设 , . 设函数是含谷函数,是它的一个含谷区间,并记的最大值为 . 若 , 且 , 求的最小值.