贵州省黔东南苗族侗族自治州2024届高三12月数学统测(一模)试卷
试卷更新日期:2024-01-02 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知复数 , , 则的实部与虚部分别为( )A、 , B、 , C、 , D、 ,2. 设集合 , , 则( )A、 B、 C、 D、3. 若某等差数列的前3项和为27,且第3项为5,则该等差数列的公差为( )A、 B、 C、3 D、44. 若 , , 则( )A、3 B、 C、5 D、5. 若平面 , 截球所得截面圆的面积分别为 , , 且球心到平面的距离为3,则球心到平面的距离为( )A、 B、2 C、 D、46. 已知是奇函数,且在上单调递减,则下列函数既是奇函数,又在上单调递增的是( )A、 B、 C、 D、7. 已知贵州某果园中刺梨单果的质量(单位:)服从正态分布 , 且 , 若从该果园的刺梨中随机选取100个单果,则质量在的单果的个数的期望为( )A、20 B、60 C、40 D、808. 是抛物线上异于坐标原点的一点,点在轴上, , 为该抛物线的焦点,则( )A、12 B、11 C、10 D、9
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 若函数 , 则( )A、的最小正周期为10 B、的图象关于点对称 C、在上有最小值 D、的图象关于直线对称10. 在正四棱台中, , , , 则( )A、该正四棱台的体积为 B、直线与底面所成的角为 C、线段的长为 D、以为球心,且表面积为的球与底面相切11. 已知是圆上一点,是圆上一点,则( )A、的最小值为2 B、圆与圆有4条公切线 C、当取得最小值时,点的坐标为 D、当时,点到直线的距离小于212. 已知函数 , .若关于的方程有3个实数解 , , , 且 , 则( )A、的取值范围是 B、的取值范围是 C、的最小值为4 D、的最小值是13
三、填空题:本题共4小题,每小题5分,共20分.
-
13. 的展开式中,的系数为.14. 向量在向量上的投影向量为 , 则.15. 烧水时,水温随着时间的推移而变化.假设水的初始温度为℃,加热后的温度函数(是常数,表示加热的时间,单位:),加热到第时,水温的瞬时变化率是℃/.16. 过双曲线的右焦点作的一条渐近线的垂线,垂足为 , 且的左顶点为 , , 则的离心率为.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 为了了解贵州省大学生是否关注原创音乐剧与性别有关,某大学学生会随机抽取1000名大学生进行统计,得到如下列联表:
男大学生
女大学生
合计
关注原创音乐剧
250
300
550
不关注原创音乐剧
250
200
450
合计
500
500
1000
(1)、从关注原创音乐剧的550名大学生中任选1人,求这人是女大学生的概率.(2)、试根据小概率值的独立性检验,能否认为是否关注原创音乐剧与性别有关联?说明你的理由.附: , 其中.
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
18. 的内角A , B , C所对的边分别为a , b , c , 且.(1)、求角;(2)、若 , 求的最小值.19. 如图,在三棱锥中,平面平面 , , , , D , E分别为 , 的中点.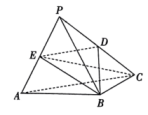 (1)、证明:平面平面.(2)、求平面与平面的夹角的余弦值.
(1)、证明:平面平面.(2)、求平面与平面的夹角的余弦值.