四川省乐山市2024届高三上学期数学(文科)12月第一次调研考试试卷
试卷更新日期:2024-01-02 类型:高考模拟
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设全集 , 集合 , , 则( )A、 B、 C、 D、2. 已知复数 , 则复数的实部为( )A、 B、 C、1 D、3. 执行右边的程序框图,则输出的( )
 A、 B、7 C、0 D、24. 如图是某几何体的三视图,其中主视图和左视图是两个全等的正方形,且边长为2,俯视图是直径为2的圆,则这个几何体的侧面积为( )
A、 B、7 C、0 D、24. 如图是某几何体的三视图,其中主视图和左视图是两个全等的正方形,且边长为2,俯视图是直径为2的圆,则这个几何体的侧面积为( )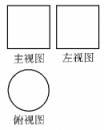 A、 B、 C、 D、5. 已知 , 则( )A、 B、 C、 D、6. 对四组数据进行统计,获得如下散点图,关于其相关系数的比较,说法正确的是( )
A、 B、 C、 D、5. 已知 , 则( )A、 B、 C、 D、6. 对四组数据进行统计,获得如下散点图,关于其相关系数的比较,说法正确的是( )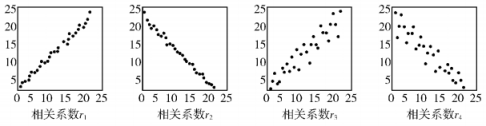 A、 B、 C、 D、7. 3个0和2个1随机排成一行,则2个1不相邻的概率为( )A、 B、 C、 D、8. 设等差数列的前n项和 , 若 , , 则( )A、18 B、27 C、45 D、639. 函数的图象大致为( )A、
A、 B、 C、 D、7. 3个0和2个1随机排成一行,则2个1不相邻的概率为( )A、 B、 C、 D、8. 设等差数列的前n项和 , 若 , , 则( )A、18 B、27 C、45 D、639. 函数的图象大致为( )A、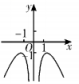 B、
B、 C、
C、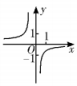 D、
D、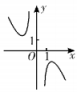 10. 地处长江上游的四川省乐山市,多年来始终树立上游意识,落实上游责任,不断提升水环境治理体系和治理能力现代化水平,为守护好这一江清水作出乐山贡献(摘自:人民网四川频道)。为了解过滤净化原理,某中学科创实践小组的学生自制多层式分级过滤器,用于将含有沙石的大渡河河水进行净化。假设经过每一层过滤可以过滤掉五分之一的沙石杂质,若要使净化后河水中沙石杂质含量不超过最初的三分之一,则最少要经过多少层的过滤?(参考数据: , )A、7 B、6 C、5 D、411. 已知函数(其中 , )在时取最大值,两条对称轴之间的最小距离为 , 则直线与曲线的交点个数为( )A、1 B、2 C、3 D、412. 已知函数定义域为R,且满足 , , , 给出以下四个命题:
10. 地处长江上游的四川省乐山市,多年来始终树立上游意识,落实上游责任,不断提升水环境治理体系和治理能力现代化水平,为守护好这一江清水作出乐山贡献(摘自:人民网四川频道)。为了解过滤净化原理,某中学科创实践小组的学生自制多层式分级过滤器,用于将含有沙石的大渡河河水进行净化。假设经过每一层过滤可以过滤掉五分之一的沙石杂质,若要使净化后河水中沙石杂质含量不超过最初的三分之一,则最少要经过多少层的过滤?(参考数据: , )A、7 B、6 C、5 D、411. 已知函数(其中 , )在时取最大值,两条对称轴之间的最小距离为 , 则直线与曲线的交点个数为( )A、1 B、2 C、3 D、412. 已知函数定义域为R,且满足 , , , 给出以下四个命题:① ②
③ ④函数的图象关于直线对称
其中正确命题的个数是( )
A、0 B、1 C、2 D、3二、填空题:本大题共4小题;每小题5分,共20分.
-
13. 命题“ , ”的否定是.14. 曲线在处的切线方程为.15. 若一个正三棱锥底面边长为1,高为 , 其内切球的表面积为.16. 已知正六边形ABCDEF边长为2,MN是正六边形ABCDEF的外接圆的一条动弦, , P为正六边形ABCDEF边上的动点,则的最小值为.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤.
-
17. 为吸引更多优秀人才来乐山干事创业,2023年10月27日,乐山市招才引智系列活动——教育人才专场在西南大学北碚校区招聘大厅举行,其中,甲、乙两名大学生参加了面试,10位评委打分如茎叶图所示:
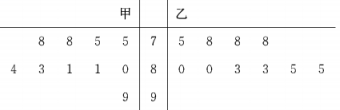 (1)、写出甲得分的中位数和乙得分的众数;(2)、现有两种方案评价选手的最终得分:
(1)、写出甲得分的中位数和乙得分的众数;(2)、现有两种方案评价选手的最终得分:方案一:直接用10位评委评分的平均值;
方案二:将10位评委评分去掉一个最低分和一个最高分之后,取剩下8个评分的平均值.请分别用以上两种方案计算两位同学的最终得分,并判断哪种评价方案更好?为什么?
18. 已知数列满足 , , 设.(1)、求 , , ;(2)、判断数列是否为等比数列,并说明理由;(3)、求的通项公式.19. 如图,在四棱锥中,底面ABCD是边长为2的正方形,底面ABCD , , 点E在棱PC上,平面EBD.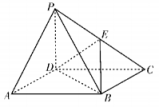 (1)、试确定点E的位置,并说明理由;(2)、是否存在实数 , 使三棱锥体积为.20. 在平面四边形ABCD中,已知 , , , .(1)、若 , 求CD;(2)、求面积的最大值.
(1)、试确定点E的位置,并说明理由;(2)、是否存在实数 , 使三棱锥体积为.20. 在平面四边形ABCD中,已知 , , , .(1)、若 , 求CD;(2)、求面积的最大值.