吉林地区普通高中2023-2024学年高三年级上学期数学第一次模拟试卷

试卷更新日期：2024-01-02 类型：高考模拟

进入出卷网下载

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个是符合题目要求．

1. 已知全集 $U = {1 ， 2 ， 3 ， 4 ， 5}$ ， $A = {1 ， 3 ， 4}$ ， $B = {2 ， 4}$ ，则 $A ∩ (C_{U} B) =$ （）

A、 ${1 ， 3}$ B、 ${2 ， 4}$ C、 ${1 ， 3 ， 5}$ D、 ${2 ， 4 ， 5}$

查看试题解析
2. 若复数 $z = \frac{2 i}{1 + 2 i}$ ，则 $z$ 的虚部是（）

A、 $\frac{4}{5}$ B、 $\frac{4}{5} i$ C、 $\frac{2}{5}$ D、 $\frac{2}{5} i$

查看试题解析
3. “ $\sqrt{m} \geq \sqrt{n}$ ”是“ $l n m \geq l n n$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知 $a = 0.3 1^{0.1}$ ， $b = 0.3 1^{0.2}$ ， $c = 0.3 2^{0.1}$ ，则（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > b > a$ D、 $c > a > b$

查看试题解析
5. 在等比数列 ${a_{n}}$ 中， $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = - \frac{11}{4}$ ， $a_{3} = - \frac{1}{4}$ ，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + \frac{1}{a_{4}} + \frac{1}{a_{5}} =$ （）

A、 $- 44$ B、 $- \frac{64}{11}$ C、 $\frac{16}{11}$ D、11

查看试题解析
6. 已知函数 $f (x)$ ， $g (x)$ 的定义域均为 $R$ ， $f (x) + f (10 - x) = 4$ ， $g (1) = 2$ 且 $g (x) + g (x + 2) = 2$ ，则 $\sum_{i = 1}^{9} [f (i) + g (i)] =$ （）

A、24 B、26 C、28 D、30

查看试题解析
7. 在直角三角形 $A B C$ 中， $A = 90 °$ 、 $△ A B C$ 的重心、外心、垂心、内心分別为 $G_{1}$ ， $G_{2}$ ， $G_{3}$ ， $G_{4}$ ，若 $\vec{A G_{i}} = λ_{i} \vec{A B} + μ_{i} \vec{A C}$ （其中 $i = 1 ， 2 ， 3 ， 4$ ），当 $λ_{i} + μ_{i}$ 取最大值时， $i =$ （）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知函数 $f (x) = 2 s i n (ω x + \frac{π}{4})$ 在区间 $(0 ， π)$ 上有且仅有4个极大值点，则正实数 $ω$ 的取值范围为（）

A、 $(\frac{13}{4} ， \frac{17}{4}]$ B、 $[\frac{13}{4} ， \frac{17}{4})$ C、 $(\frac{25}{4} ， \frac{33}{4}]$ D、 $[\frac{25}{4} ， \frac{33}{4})$

查看试题解析

二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 已知函数 $f (x) = l o g_{a} x$ （ $a > 0$ ，且 $a \neq 1$ ）的反函数为 $g (x)$ ，则（）

A、 $g (x) = a^{x}$ （ $a > 0$ ，且 $a \neq 1$ ）且定义域是 $(0 ， + \infty)$ B、若 $f (9) = 2$ ，则 $g (3) = 27$ C、函数 $f (x)$ 与 $g (x)$ 的图象关于直线 $y = x$ 对称 D、函数 $f (x)$ 与 $g (x)$ 的图象的交点个数可能为0，1，2，3

查看试题解析
10. 口袋中装有大小质地完全相同的白球和黑球各2个，从中不放回的依次取出2个球，事件 $A =$ “取出的两球同色”，事件 $B =$ “第一次取出的是白球”，事件 $C =$ “第二次取出的是白球”，事件 $D =$ “取出的两球不同色”，则（）

A、 $P (B) = \frac{1}{2}$ B、 $B$ 与 $C$ 互斥 C、 $A$ 与 $B$ 相互独立 D、 $A$ 与 $D$ 互为对立

查看试题解析
11. 等差数列 ${a_{n}}$ 与 ${b_{n}}$ 的前 $n$ 项和分别是 $S_{n}$ 与 $T_{n}$ ，且 $\frac{S_{n}}{T_{n}} = \frac{4 n - 25}{2 n - 5} (n \in N^{*})$ ，则（）

A、 $\frac{a_{3}}{b_{3}} = - 13$ B、 $\frac{a_{3}}{b_{4}} = - \frac{5}{9}$ C、 $\frac{S_{n}}{T_{n}}$ 的最大值是17 D、 $\frac{S_{n}}{T_{n}}$ 最小值是7

查看试题解析
12. 中华人民共和国国旗是五星红旗，国旗上每个五角星之所以看上去比较美观，是因其图形中隐藏着黄金分割数．连接正五边形的所有对角线能够形成一个标准的正五角星，正五角星中每个等腰三角形都是黄金三角形．黄金三角形分两种：一种是顶角为 $36 °$ 的等腰三角形，其底边与一腰的长度之比为黄金比 $\frac{\sqrt{5} - 1}{2}$ ；一种是顶角为 $108 °$ 的等腰三角形，其一腰与底边的长度之比为黄金比 $\frac{\sqrt{5} - 1}{2}$ ．如图，正五角星 $A B C D E$ 中， $A G = 2$ ，记 $< \vec{A G} ， \vec{A F} > = θ$ ，则（）

A、 $\vec{A G} = \vec{F I}$ B、 $\vec{A G} \cdot \vec{A F} = \sqrt{5} + 1$ C、 $\vec{A G}$ 在 $\vec{A F}$ 上的投影向量为 $\frac{\sqrt{5} + 1}{2} \vec{A F}$ D、 $c o s 2 θ + c o s 4 θ + c o s 6 θ + ⋯ + c o s 2024 θ = - \frac{1}{2}$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分．其中第15题的第一个空填对得2分，第二个空填对得3分．

13. 已知 $x > 1$ ，则 $x + \frac{4}{x - 1}$ 的最小值为．

查看试题解析
14. 已知tanθ=2，则sinθcosθ= ．

查看试题解析
15. 吉林市一中学有男生900人，女生600人．在“书香校园”活动中，为了解全校学生的读书时间，按性别比例分层随机抽样的方法抽取100名学生，其中男生、女生每天读书时间的平均值分别为60分钟和80分钟，方差分别为10和15．结合上述数据估计该校学生每天读书时间的平均值为分钟，方差为．

查看试题解析
16. 已知函数 $f (x) = {\begin{cases} \frac{e^{x}}{x - 1} ， x > 0 且 x \neq 1 ， \\ - f (- x) ， x < 0 且 x \neq - 1 ， \end{cases}$ 若函数 $g (x) = f^{2} (x) - m f (x) - e^{4}$ 有4个零点．则实数 $m$ 的取值范围是．

查看试题解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

17. 已知向量 $\vec{a} = (\sqrt{3} s i n x ， c o s x)$ ， $\vec{b} = (c o s x ， c o s x)$ ．

(1)、若 $\vec{a} ∥ \vec{b}$ 且 $x \in (0 ， π)$ ，求 $x$ ；

(2)、若函数 $f (x) = \vec{a} \cdot \vec{b} - \frac{1}{2}$ ，求 $f (x)$ 的单调递增区间．

查看试题解析
18. 已知函数 $f (x) = - 2 x + l n x$ ．

(1)、求曲线 $y = f (x)$ 在 $(1 ， f (1))$ 处的切线方程；

(2)、若对 $\forall x \in (0 ， + \infty)$ ， $f (x) \leq a x^{2} - 2 x$ 恒成立．求实数 $a$ 的取值范围．

查看试题解析
19. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 2$ ， $S_{n} = a_{n + 1}$ ．

(1)、请在①②中选择一个作答，并把序号填在答题卡对应位置的横线上，①求数列 ${a_{n}}$ 的通项公式；②求 $S_{n}$ ；

(2)、令 $b_{n} = \frac{S_{n}}{(a_{n + 1} - 1) (a_{n + 2} - 1)}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ，并证明 $T_{n} < 1$ ．

查看试题解析
20. 近几年以华为为代表的中国高科技企业正在不断突破科技封锁．多项技术已经“遥遥领先”．国产光刻机作为芯片制造的核心设备，也已经取得了突飞猛进的发展．已知一芯片生产商用某国产光刻机生产的 $Q$ 型芯片经过十项指标全面检测后，分为Ⅰ级和Ⅱ级，两种芯片的某项指标的频率分布如图所示：
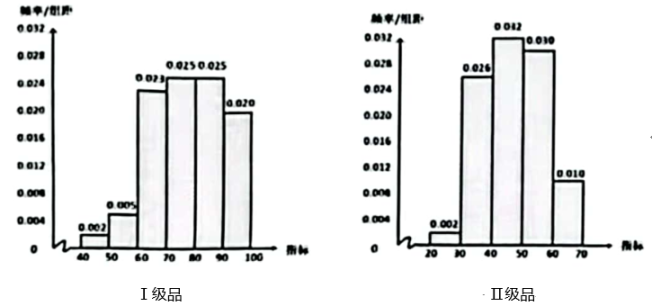
若只利用该指标制定一个标准，需要确定临界值 $c$ ，将该指标大于 $c$ 的产品应用于 $A$ 型手机，小于或等于 $c$ 的产品应用于 $B$ 型手机．假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率．

(1)、求 $Q$ 型芯片Ⅰ级品该项指标的第70百分位数；

(2)、当临界值 $c = 65$ 时，求 $Q$ 型芯片Ⅱ级品应用于 $A$ 型手机的概率；

(3)、已知 $c \in [50 ， 60]$ ，现有足够多的 $Q$ 型芯片Ⅰ级品、Ⅱ级品，分别应用于 $A$ 型于机、 $B$ 型手机各1万部的生产：
方案一：直接将 $Q$ 型芯片Ⅰ级品应用于 $A$ 型手机，其中该指标小于等于临界值 $c$ 的芯片会导致芯片生产商每部手机损失700元；直接将 $Q$ 型芯片Ⅱ级品应用于 $B$ 型手机，其中该指标大于临界值 $c$ 的芯片，会导致芯片生产商每部手机损失300元；
方案二：重新检测 $Q$ 型芯片Ⅰ级品，Ⅱ级品，会避免方案一的损失费用，但检测费用共需要101万元；
请从芯片生产商的成本考虑，选择合理的方案．

查看试题解析
21. 已知 $△ A B C$ 的三个角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ， $c (c o s A - \sqrt{3} s i n A) = b - 2 a$ ， $c = 2$ ．

(1)、求角 $C$ ；

(2)、若 $A B = B C$ ，在 $△ A B C$ 的边 $A C$ 和 $B C$ 上分别取点 $D$ ， $E$ ，将 $△ C D E$ 沿线段 $D E$ 折叠到平面 $A B E$ 后，顶点 $C$ 恰好落在边 $A B$ 上（设为点 $P$ ），设 $C E = x$ ，当 $C E$ 取最小值时，求 $△ P B E$ 的面积．

查看试题解析
22. 已知函数 $f (x) = e^{x} + m s i n x$ ．

(1)、若函数 $f (x)$ 在 $(0 ， π)$ 上单调递增，求正实数 $m$ 的取值范围；

(2)、求证：当 $m = 1$ 时， $f (x)$ 在 $(- π ， + \infty)$ 上存在唯一极小值点 $x_{0}$ ，且 $- 1 < f (x_{0}) < 0$ ．

查看试题解析