广东省韶关市2024届高三上学期数学第一次模拟考试试卷
试卷更新日期:2024-01-02 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知复数满足 , 则( )A、 B、 C、 D、2. 已知集合 , 则( )A、 B、 C、 D、3. 已知圆锥的母线长为 , 其侧面展开图为一个半圆,则该圆锥的底面半径为( )A、 B、 C、 D、4. 函数在上单调递减,则实数取值范围是( )A、 B、 C、 D、5. 某一物质在特殊环境下的温度变化满足:(为时间,单位为为特殊环境温度,为该物质在特殊环境下的初始温度,为该物质在特殊环境下冷却后的温度),假设一开始该物质初始温度为 , 特殊环境温度是 , 则经过 , 该物质的温度最接近( )(参考数据:)A、 B、 C、 D、6. 已知椭圆的左、右焦点分别为 , 过点且垂直于轴的直线与椭圆交于两点,若为等边三角形,则椭圆的离心率为( )A、 B、 C、 D、7. 已知 , 则的值为( )A、 B、 C、 D、8. 已知是定义在上且不恒为零的函数,对于任意实数满足 , 若 , 则( )A、 B、 C、 D、
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 已知圆 , 点 , 下列命题正确的是( )A、圆的圆心为 B、过点的直线可能与圆相切 C、圆上的点到点距离的最大值为 D、若以为圆心的圆和圆内切,则圆的半径为10. 数据的平均数为 , 方差为 , 数据的平均数为 , 方差为 , 其中满足关系式: , 则( )A、 B、数据的平均数为 C、若数据 , 则 D、若 , 数据不全相等,则样本点的成对样本数据的样本相关系数为111. 已知函数,的部分图象如图所示,则( )
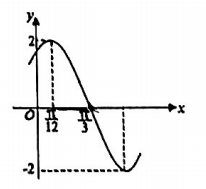 A、 B、将的图象向右平移个单位,得到的图象 C、 , 都有 D、若方程在上有两个不相等的实数根,则实数12. 已知是的导函数,则( )A、是周期函数 B、的一条对称轴是 C、在内有两个不同的零点 D、在内有两个不同的极值点
A、 B、将的图象向右平移个单位,得到的图象 C、 , 都有 D、若方程在上有两个不相等的实数根,则实数12. 已知是的导函数,则( )A、是周期函数 B、的一条对称轴是 C、在内有两个不同的零点 D、在内有两个不同的极值点三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知 , 则与的夹角为 .14. 现有五人排成一列,其中与相邻,不排在两边,则共有种不同的排法(用具体数字作答).15. 已知双曲线的左、右焦点分别为 , 以为直径的圆与双曲线在第一、三象限的交点分别为 , 设四边形的周长为 , 面积为 , 则 .16. 四面体的棱长只能是1或3,但该四面体不是正四面体,则该四面体的体积最大值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 在中,内角的对边分别为 .(1)、求;(2)、若的面积为 , 求的周长.18. 如图,在直三棱柱中, .
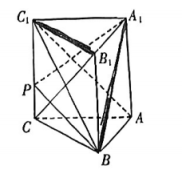 (1)、证明:;(2)、若点在棱上, , 求平面与平面夹角的余弦值.19. 已知数列的前项和满足 .(1)、证明:数列是等差数列;(2)、设 , 若成等比数列,求数列的前项和 .20. 有一个质地均匀的正方体骰子与一个有61个格子的矩形方格图,矩形方格图上从0,1,2,…,60依次标号.一个质点位于第0个方格中,现有如下游戏规则:先投掷骰子,若出现1点或2点,则质点前进1格,否则质点前进2格,每次投掷的结果互不影响.(1)、求经过两次投掷后,质点位于第4个格子的概率;(2)、若质点移动到第59个格子或第60个格子时,游戏结束,设质点移动到第个格子的概率为 , 求和的值.
(1)、证明:;(2)、若点在棱上, , 求平面与平面夹角的余弦值.19. 已知数列的前项和满足 .(1)、证明:数列是等差数列;(2)、设 , 若成等比数列,求数列的前项和 .20. 有一个质地均匀的正方体骰子与一个有61个格子的矩形方格图,矩形方格图上从0,1,2,…,60依次标号.一个质点位于第0个方格中,现有如下游戏规则:先投掷骰子,若出现1点或2点,则质点前进1格,否则质点前进2格,每次投掷的结果互不影响.(1)、求经过两次投掷后,质点位于第4个格子的概率;(2)、若质点移动到第59个格子或第60个格子时,游戏结束,设质点移动到第个格子的概率为 , 求和的值.