四川省成都市2024届高三上学期数学(理科)12月第一次诊断性检测试卷
试卷更新日期:2024-01-02 类型:月考试卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 二项式的展开式中x的系数为( )A、1 B、3 C、5 D、152. 普法知识宣传小组打算从某小区的2000人中抽取25人进行法律知识培训,拟采取系统抽样方式,为此将他们一一编号为1~2000,并对编号由小到大进行分段,假设从第一个号码段中随机抽出的号码是2,那么从第三个号码段中抽出的号码为( )A、52 B、82 C、162 D、2523. 已知复数(i为虚数单位),则z的虚部为( )A、 B、1 C、 D、i4. 若数列满足 , , 则( )A、6 B、14 C、22 D、375. 已知向量 , , 则( )A、 B、 C、 D、6. 若实数x , y满足 , 则的最小值为( )A、0 B、 C、 D、17. 已知函数的大致图象如图所示,则的解析式可以为( )
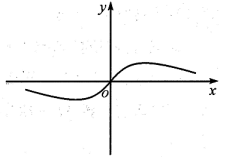 A、 B、 C、 D、8. 已知平面 , , , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 若 , , , 则( )A、 B、 C、 D、10. 已知 , 且 , 则( )A、 B、 C、 D、或11. 若 , 恒成立,则实数a的最大值为( )A、e B、2 C、1 D、12. 已知圆经过椭圆的两个焦点 , , 圆C和椭圆在第二象限的交点为N , , 则椭圆的离心率为( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知平面 , , , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 若 , , , 则( )A、 B、 C、 D、10. 已知 , 且 , 则( )A、 B、 C、 D、或11. 若 , 恒成立,则实数a的最大值为( )A、e B、2 C、1 D、12. 已知圆经过椭圆的两个焦点 , , 圆C和椭圆在第二象限的交点为N , , 则椭圆的离心率为( )A、 B、 C、 D、二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.
-
13. 已知集合 , , 则.14. 曲线在点处的切线方程为.15. 记为等差数列的前n项和.若 , 且 , , 成等比数列,则的值为.16. 已知 , 底面半径的圆锥内接于球O , 则经过S和中点的平面截球O所得截面面积的最小值为.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 如图,正四棱柱中,M为的中点, , .
 (1)、求证:平面;(2)、求二面角的余弦值.18. 某校高中阶段实行体育模块化课程教学,在高一年级开设了篮球和羽毛球两个模块课程,从该校高一年级随机抽取的100名男生和100名女生中,统计出参加上述课程的情况如下:
(1)、求证:平面;(2)、求二面角的余弦值.18. 某校高中阶段实行体育模块化课程教学,在高一年级开设了篮球和羽毛球两个模块课程,从该校高一年级随机抽取的100名男生和100名女生中,统计出参加上述课程的情况如下:男生
女生
总计
参加篮球模块课程人数
60
20
80
参加羽毛球模块课程人数
40
80
120
总计
100
100
200
(1)、根据上述列联表,是否有99.9%的把握认为该校高一年级体育模块化课程的选择与性别有关;(2)、根据抽取的200名学生的模块化课程成绩,每个模块课程的前3名获得参加体育模块化教学推广大使的评选资格,若在有评选资格的6名学生中随机选出2人作为体育模块化课程教学的推广大使,记这两人中来自篮球模块化课程的人数为X , 求X的分布列和期望.附:
0.025
0.010
0.005
0.001
5.024
6.635
7.879
10.828
19. 已知函数.在锐角中,角A , B , C的对边分别是a , b , c , 且满足.(1)、求A的值;(2)、若 , 求的取值范围.20. 已知抛物线的焦点为F.(1)、已知过点F的直线与抛物线C相交于A , B两点,求证:以为直径的圆与直线相切;(2)、若直线交抛物线C于P , Q两点,当的面积为2时,求直线的方程.21. 已知函数 , .(1)、求函数的单调性;(2)、当时,求证:.请考生在第22,23题中任选择一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.