广东省江门市鹤山市重点中学2023-2024学年高二上学期数学第二阶段考试试卷
试卷更新日期:2024-01-02 类型:月考试卷
一、单项选择题:本大题共8题,每题5分,共40分.
-
1. 已知向量 , 且与共线,则( )A、1 B、2 C、-1 D、-22. 双曲线的渐近线方程为( )A、 B、 C、 D、3. 设是等差数列的前项和,若 , 则( )A、36 B、45 C、54 D、634. 圆与圆的公切线条数为( )A、1 B、2 C、3 D、45. 点关于直线的对称点的坐标为( )A、 B、 C、 D、6. 设等差数列 , 的前项和分别为 , , 若 , 则( )A、 B、 C、 D、7. 南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为 , 将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()( )A、 B、 C、 D、8. 已知椭圆上存在点 , 使得 , 其中 , 分别为椭圆的左、右焦点,则该椭圆的离心率的取值范围是( )A、 B、 C、 D、
二、多项选择题:本大题共4题,每题5分,共20分.
-
9. 已知等差数列的前项和为 , 公差.若 , 则( )A、 B、 C、 D、10. 如图,在正方体中,为的中点,则( )
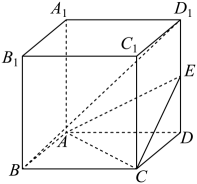 A、平面 B、 C、若正方体的棱长为 , 则点到平面的距离为 D、直线与平面所成角的正弦值为11. 已知曲线上任意一点到直线的距离比它到点的距离大 , 则下列结论正确的是( )A、曲线的方程为 B、若曲线上的一点到点的距离为 , 则点的纵坐标是4 C、已知曲线上的两点 , 到点的距离之和为10,则线段的中点横坐标是 D、已知 , 是曲线上的动点,则的最小值为512. 已知点是圆上一动点,则下列说法正确的是( )A、的最小值是0 B、的最大值为1 C、的最大值为 D、的最小值为
A、平面 B、 C、若正方体的棱长为 , 则点到平面的距离为 D、直线与平面所成角的正弦值为11. 已知曲线上任意一点到直线的距离比它到点的距离大 , 则下列结论正确的是( )A、曲线的方程为 B、若曲线上的一点到点的距离为 , 则点的纵坐标是4 C、已知曲线上的两点 , 到点的距离之和为10,则线段的中点横坐标是 D、已知 , 是曲线上的动点,则的最小值为512. 已知点是圆上一动点,则下列说法正确的是( )A、的最小值是0 B、的最大值为1 C、的最大值为 D、的最小值为三、填空题:本大题共4题,每题5分,共20分.
-
13. 若向量 , , 则 .14. 若两条平行直线与之间的距离是 , 则 .15. 已知数列的前项和 , 则数列的通项公式为.16. 已知正边长为1,将绕旋转至 , 使得平面平面 , 则三棱锥的外接球表面积为 .
四、解答题:本大题共6题,第17题10分,18至22题每题12分,共70分.
-
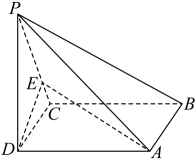
17. 已知的顶点.(1)、求边上的中线所在直线的方程;(2)、求经过点 , 且在轴上的截距和轴上的截距相等的直线的方程.18. 如图,在平行六面体中,以顶点A为端点的三条棱长度都为2,且两两夹角为 .
 (1)、求的长;(2)、求与所成角的余弦值.19. 在平面直角坐标系内,动点与定点的距离和它到定直线的距离的比是.(1)、求动点的轨迹方程.(2)、若为动点的轨迹上一点,且 , 求三角形的面积.
(1)、求的长;(2)、求与所成角的余弦值.19. 在平面直角坐标系内,动点与定点的距离和它到定直线的距离的比是.(1)、求动点的轨迹方程.(2)、若为动点的轨迹上一点,且 , 求三角形的面积.