浙江省杭州学军名校2023-2024学年高一上学期数学12月月考试卷

试卷更新日期：2024-01-02 类型：月考试卷

进入出卷网下载

一、单项选择题（每小题5分，共40分）

1. 集合 $M = {x | x = \frac{k π}{2} + \frac{π}{4} ， k \in Z}$ ， $N = {x | x = \frac{k π}{4} + \frac{π}{2} ， k \in Z}$ ，则（）

A、 $M = N$ ； B、 $M \subset N$ ； C、 $M \supset N$ ； D、 $M \cap N = \emptyset$ ．

查看试题解析
2. 点 $P$ 从 $(0 ， - 1)$ 出发，沿着单位圆的边界顺时针运动 $\frac{8 π}{3}$ 弧长到达点 $Q$ ，则点 $Q$ 的坐标为（）

A、 $(\frac{\sqrt{3}}{2} ， \frac{1}{2})$ B、 $(\frac{1}{2} ， \frac{\sqrt{3}}{2})$ C、 $(- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ D、 $(- \frac{\sqrt{3}}{2} ， \frac{1}{2})$

查看试题解析
3. 已知 $α \in (0 ， π)$ ，若 $c o s (\frac{π}{6} - α) = - \frac{\sqrt{2}}{4}$ ，则 $s i n (α + \frac{5 π}{6})$ 的值为（）

A、 $- \frac{\sqrt{14}}{4}$ B、 $\frac{\sqrt{2}}{4}$ C、 $- \frac{\sqrt{2}}{4}$ D、 $\frac{\sqrt{14}}{4}$

查看试题解析
4. 中国折扇有着深厚的文化底蕴.用黄金分割比例设计一把富有美感的纸扇，如图所示，在设计折扇的圆心角 $θ$ 时，可把折扇考虑为从一圆形（半径为 $r$ ）分割出来的扇形，使扇形的面积 $S_{1}$ 与圆的面积的乘积等于剩余面积 $S_{2}$ 的平方.则扇形的圆心角 $θ$ 为（）

A、 $\frac{(\sqrt{5} - 1) π}{2}$ B、 $(\sqrt{5} - 2) π$ C、 $(3 - \sqrt{5}) π$ D、 $\frac{(\sqrt{5} + 1) π}{4}$

查看试题解析
5. 若奇函数 $f (x)$ 和偶函数 $g (x)$ 满足 $f (x) + g (x) = 3^{x} + x^{3} + 2$ ，则 $f (1) + g (0) =$ （）

A、 $\frac{7}{3}$ B、 $\frac{8}{3}$ C、 $\frac{19}{3}$ D、 $\frac{16}{3}$

查看试题解析
6. 若函数 $f (x) = l o g_{\frac{1}{2}} (x^{2} + a x - 2 a)$ 在 $[1 ， + \infty)$ 上单调递减，则实数 $a$ 的取值范围是（）．

A、 $(- \infty ， - 2]$ B、 $[- 2 ， + \infty)$ C、 $[- 2 ， 1)$ D、 $[- 2 ， - 1]$

查看试题解析
7. 已知 $t a n α = \frac{1}{3} ， t a n β = - \frac{1}{7} ，$ 且 $α ， β \in (0 ， π)$ ，则 $2 α - β$ =（）

A、 $\frac{π}{4}$ B、 $- \frac{π}{4}$ C、 $- \frac{3 π}{4}$ D、 $- \frac{3 π}{4}$ 或 $\frac{π}{4}$

查看试题解析
8. 对于函数 $f (x)$ ，若 $f (x_{0}) = x_{0}$ ，则称 $x_{0}$ 为函数 $f (x)$ 的“不动点”：若 $f (f (x_{0})) = x_{0}$ ，则称 $x_{0}$ 为函数 $f (x)$ 的“稳定点”．已知 $f (x) = x^{2} + a$ 的稳定点都是它的不动点，则实数 $a$ 的范围是（）．

A、 $(- \frac{3}{4} ， + \infty)$ B、 $[- \frac{3}{4} ， + \infty)$ C、 $(- \frac{3}{4} ， \frac{1}{4}]$ D、 $[- \frac{3}{4} ， \frac{1}{4}]$

查看试题解析

二、多项选择题（每小题5分，部分选对得2分，共20分）

9. 设全集为R，在下列条件中，满足 $B ⊆ A$ 的充要条件的有（）

A、 $A ∩ B = A$ B、 $(∁_{R} A) \cap B = R$ C、 $∁_{R} A \subseteq ∁_{R} B$ D、 $A ∪ (∁_{R} B) = R$

查看试题解析
10. 函数 $f (x) = x l n (x + π) - 1$ 的零点所在的区间可能为（）

A、 $(- 3 ， - 2)$ B、 $(- 2 ， - 1)$ C、 $(0 ， 1)$ D、 $(1 ， 2)$

查看试题解析
11. 在 $△ A B C$ 中， $s i n A = \frac{\sqrt{5}}{5} ， s i n B = \frac{\sqrt{10}}{10}$ ，则 $s i n (A - B)$ 的值可能是（）

A、 $- \frac{\sqrt{2}}{10}$ B、 $\frac{\sqrt{2}}{10}$ C、 $- \frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
12. 已知函数 $f (x) = s i n (ω x + \frac{π}{4}) (ω > 0)$ 在区间 $[0 ， π]$ 上有且仅有4条对称轴，则下面给出的结论中，正确的是（）．

A、 $ω$ 的取值范围是 $[\frac{13}{4} ， \frac{17}{4})$ B、 $f (x)$ 的最小正周期可能是2 C、 $f (x)$ 在区间 $(0 ， π)$ 上可能恰有4个零点 D、 $f (x)$ 在区间 $(0 ， \frac{π}{12})$ 上可能单调递增

查看试题解析

三、填空题（每小题5分，共20分）

13. 对任意 $a > 0$ 且 $a \neq 1$ ，函数 $f (x) = a^{x + 1} + 1$ 的图象都过定点 $P$ ，且 $P$ 在角 $θ$ 的终边上，则 $c o s θ =$ ．

查看试题解析
14. 已知函数 $f (x) = a s i n (π x + α) + b c o s (π x + β) + x$ ，且 $f (2022) = 0$ ，则 $f (2023) =$ ．

查看试题解析
15. 若关于 $x$ 的不等式 $2^{2 x + 1} - (m + 1) \cdot 2^{x} + 18 \leq 0$ 在 $[0 ， 1]$ 上有解，则实数 $m$ 的最小值为．

查看试题解析
16. 已知 $f (x) = \sin (ω x + φ + \frac{π}{3}) (ω > 0)$ 同时满足下列三个条件：① $T = π$ ；② $y = f (x - \frac{π}{3})$ 是奇函数；③ $f (0) < f (\frac{π}{6})$ .若 $f (x)$ 在 $[0 ， t)$ 上没有最小值，则实数 $t$ 的取值范围是.

查看试题解析

四、解答题（共70分）

17. 已知关于 $x$ 的不等式 $x^{2} - \sqrt{a b} \cdot x + \frac{b - 1}{4} \leq 0$ ．

(1)、当 $a = 1 ， b = 4$ 时，求不等式的解集；

(2)、若不等式仅有一个解，求 $\frac{4}{a} + b$ 的最小值．

查看试题解析
18. 某商品近一个月内（30天）预计日销量 $y = f (t)$ （件）与时间t(天)的关系如图1所示，单价 $y = g (t)$ （万元/件）与时间t(天)的函数关系如图2所示，（t为整数）

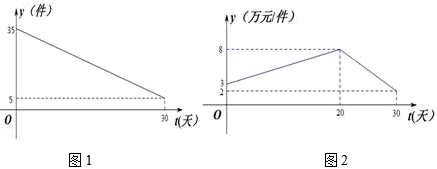(1)、试写出 $f (t)$ 与 $g (t)$ 的解析式；

(2)、求此商品日销售额的最大值？

查看试题解析
19. 已知函数 $f (x) = 3 c o s (\frac{π}{3} - 2 x) - 2$ ．

(1)、求函数的最小正周期、对称中心、单调减区间；

(2)、若定义在区间 $[- \frac{π}{6} ， \frac{π}{4}]$ 上的函数 $h (x) = a f (x) + b$ 的最大值为6，最小值为 $- 3$ ，求实数 $a 、 b$ 的值．

查看试题解析
20. 已知函数 $f (x) = l o g_{a} \frac{b + x}{2 - x}$ 是奇函数，且 $f (1) = - 1$ ．

(1)、求实数 $a$ 、 $b$ 的值；

(2)、求函数 $y = f (2^{x})$ 在 $(3 - l o g_{2} 5 ， 1)$ 的值域；

(3)、若 $f (t^{2} - 3) + f (1 - t) > 0$ ，求实数 $t$ 的取值范围．

查看试题解析
21. 若关于 $x$ 的两个不等式 $f (x) < 0$ 和 $g (x) < 0$ 的解集分别为 $(m ， n)$ 和 $(\frac{1}{n} ， \frac{1}{m})$ ，则称这两个不等式为“对偶不等式”．

(1)、已知 $x^{2} - 4 c o s θ \cdot x + 2 < 0$ 与 $a x^{2} - 4 \sqrt{3} s i n θ \cdot x + 1 < 0$ 为对偶不等式．求 $a 、 θ$ 的值；

(2)、若 $(\sqrt{2} + 1) x^{2} - 2 \sqrt{2} t a n α \cdot x + 1 < 0$ 与 $b x^{2} - 2 \sqrt{2} t a n β \cdot x + \sqrt{2} - 1 < 0$ 为对偶不等式，且 $α 、 β \in (0 ， \frac{π}{2})$ ．求 $α - β$ 的最大值．

查看试题解析
22. 若函数 $f (x)$ 满足：对任意 $x \in R ， f (x) = f (\frac{3 π}{2} - x) = f (\frac{3 π}{2} + x)$ ，则称 $f (x)$ 为“ $M$ 函数”．

(1)、判断 $f_{1} (x) = s i n (\frac{4}{3} x + \frac{π}{2}) ， f_{2} (x) = | t a n \frac{2}{3} x |$ 是不是 $M$ 函数（直接写出结论）；

(2)、已在函数 $f (x)$ 是 $M$ 函数，且当 $x \in [0 ， \frac{3 π}{4}]$ 时， $f (x) = s i n x$ ．求 $f (x)$ 在 $[\frac{3}{2} π ， 3 π]$ 的解析式；

(3)、在（2）的条件下， $x \in [0 ， 6 π]$ 时，关于 $x$ 的方程 $f (x) = a$ （ $a$ 为常数）有解，求该方程所有解的和 $S$ ．

查看试题解析