重庆市开州区德阳教育集团2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（共12小题，每小题4分，共48分）

1. $- 2$ 的绝对值是（）

A、 $2$ B、 $- 2$ C、 $2$ 或 $- 2$ D、 $\frac{1}{2}$ 或 $- \frac{1}{2}$

查看试题解析
2. 下列运算中正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 $2 a + 3 b = 5 a b$ C、 $a^{2} + a^{2} = a^{4}$ D、 $- 3 (a - b) = - 3 a + 3 b$

查看试题解析
3. 若 $x + 2 y = 6$ ，则多项式 $2 x + 4 y - 5$ 的值为（　　）

A、5 B、6 C、7 D、8

查看试题解析
4. 如图，直线a∥b，直角三角形的直角顶点在直线b上，已知∠1＝42°，则∠2的度数是（）

A、42° B、52° C、48° D、58°

查看试题解析
5. 已知 $m = \sqrt{61} - 1$ ，那么 $m$ 的取值范围是（）

A、 $8 < m < 9$ B、 $7 < m < 8$ C、 $6 < m < 7$ D、 $5 < m < 6$

查看试题解析
6. 如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（）

A、8 B、9 C、10 D、11

查看试题解析
7. 如图， $A C$ 与 $D B$ 相交于 $E$ ，且 $B E = C E$ ，如果添加一个条件还不能判定 $△ A B E$ ≌ $△ D C E$ ，则添加的这个条件是（）．

A、 $A C = D B$ B、 $∠ A = ∠ D$ C、 $∠ B = ∠ C$ D、 $A B = D C$

查看试题解析
8. 下列图案都是有若干个全等的等边三角形按一定规律摆放而成，依此规律，第10个图中等边三角形的个数为（）

A、28 B、32 C、36 D、40

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ， $D E ⊥ A B$ 于 $E$ ， $B E = 2 ， B C = 6$ ，则 $△ B D E$ 的周长为（　　）

A、6 B、8 C、10 D、14

查看试题解析
10. 如图， $A E ⊥ A B$ 且 $A E = A B ， B C ⊥ C D$ 且 $B C = C D$ ，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）

A、50 B、62 C、65 D、68

查看试题解析
11. 若数m使关于x的方程3x+m=x-5 的解为负数，且使关于y的不等式 ${\begin{array}{l} \frac{y + 2}{3} - \frac{y}{2} ＜ 1 \\ 3 (y - m) \geq 0 \end{array}$ 组的解集为y >-2，则符合条件的所有整数m的和为（　　）

A、-14 B、-9 C、-7 D、7

查看试题解析
12. 如图，点 $C$ 在线段 $A B$ 上， $D A ⊥ A B$ ， $E B ⊥ A B$ ， $F C ⊥ A B$ ，且 $D A = B C$ ， $E B = A C$ ， $F C = A B$ ， $∠ A F B = 51 °$ ，则 $∠ D F E$ 的度数为（　　）

A、 $38 °$ B、 $39 °$ C、 $40 °$ D、 $41 °$

查看试题解析

二、填空题（共6小题，每小题4分，共24分）

13. 2021年重庆博物馆共接待游客3300000人次，将数3300000用科学记数法表示为．

查看试题解析
14. 已知△ABC的三边长a、b、c ，化简|a＋b﹣c|﹣|b﹣a﹣c|的结果是．

查看试题解析
15. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G ， D、C分别在M、N的位置上，若∠EFG＝49°，则∠2﹣∠1＝．

查看试题解析
16. 如图，在 $△ O A B$ 和△OCD中， $O A = O B$ ， $O C = O D$ ， $∠ A O B = ∠ C O D = 40 °$ ，连接 $A C$ ， $B D$ 交于点 $M$ ，连接 $O M$ ．则 $∠ C M B$ 的度数为°．

查看试题解析
17. 如图， $∠ M O N = 90 °$ ，点A ， B分别在射线 $O M ， O N$ 上运动， $B E$ 平分 $∠ N B A$ ， $B E$ 的反向延长线与 $∠ B A O$ 的平分线交于点C ，则 $∠ C =$ °．

查看试题解析
18. 火锅是重庆的一张名片，深受广大市民的喜爱.重庆某火锅店采取堂食、外卖、店外摆摊（简称摆摊）三种方式经营，6月份该火锅店堂食、外卖、摆摊三种方式的营业额之比为3：5：2.随着促进消费政策的出台，该火锅店老板预计7月份总营业额会增加，其中摆摊增加的营业额占总增加的营业额的 $\frac{2}{5}$ ，则摆摊的营业额将达到7月份总营业额的 $\frac{7}{20}$ ，为使堂食、外卖7月份的营业额之比为8：5，则7月份外卖还需增加的营业额与7月份总营业额之比是.

查看试题解析

三、解答题（共8小题，19-25题各10分，26题8分，共78分）

19.

(1)、计算： $| - 2 | - \sqrt{25} + \sqrt[3]{- 8} + \sqrt{{(- 3)}^{2}}$ ；

(2)、先去括号，再合并同类项： $2 (2 b - 3 a) + 3 (2 a - 3 b)$ ．

查看试题解析
20. 如图，在△ABC中，∠BAC=50°，∠C=60°，AD⊥BC，

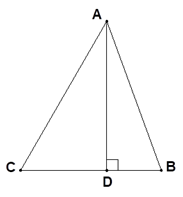(1)、用尺规作图作∠ABC的平分线BE，且交AC于点E，交AD于点F（不写作法，保留作图痕迹）；

(2)、求∠BFD的度数.

查看试题解析
21. 某公司调查某中学学生对其环保产品的了解情况，随机抽取该校部分学生进行问卷，结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型，分别记为 $A ， B ， C ， D$ ，根据调查结果绘制了如下尚不完整的统计图.

(1)、本次问卷共随机调查了名学生，扇形统计图中 $m =$

(2)、请根据数据信息，补全条形统计图；

(3)、若该校有1000名学生，估计选择“非常了解”、“比较了解”共约有多少人？

查看试题解析
22. 如图，AB＝CD，DE⊥AC，BF⊥AC，点E，F是垂足，AE＝CF，求证：

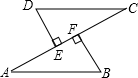(1)、△ABF≌△CDE；

(2)、AB∥CD.

查看试题解析
23. 如图，在△ABC中，AB＝AC，∠BAC＝90°，∠1＝∠2，CE⊥BD交BD的延长线于点E.求证：BD＝2CE.

查看试题解析
24. 橙子中含有丰富的维生素C和类黄酮具有很强的抗氧化性，可以起到减少皱纹、美白肌肤的美容功效，受到广大女性消费者的喜爱.某水果店以5元/千克的价格购进一批橙子，很快售罄，该店又再次购进，第二次进货价格比第一次每千克便宜了2元，两次一共购进600千克，且第二次进货的花费是第一次进货花费的1.2倍

(1)、该水果店两次分别购进了多少千克的橙子?

(2)、售卖中，第一批橙子在其进价的基础上加价a%进行定价，第二批橙子因为进价便宜，因此以第一批橙子的定价再打八折进行销售．销售时，在第一批橙子中有5%的橙子变质不能出售，在第二批橙子中有10%的橙子变质不能出售，该水果店售完两批橙子能获利2102元，求a的值

查看试题解析
25. 若一个三位数t＝ $a b c$ （其中a、b、c不全相等且都不为0），重新排列各数位上的数字必可得到一个最大数和一个最小数，此最大数和最小数的差叫做原数的差数，记为T（t）．例如，539的差数T（539）＝953﹣359＝594．

(1)、根据以上方法求出T（268）＝， T（513）＝；

(2)、已知三位数 $a 1 b$ （其中a＞b＞1）的差数T（ $a 1 b$ ）＝495，且各数位上的数字之和为3的倍数，求所有符合条件的三位数的值．

查看试题解析
26.

(1)、如图 $1$ ，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B = ∠ D = 90 °$ ， $E 、 F$ 分别是边 $B C 、 C D$ 上的点，且 $∠ E A F = \frac{1}{2} ∠ B A D$ ，线段 $E F 、 B E 、 F D$ 之间的关系是；（不需要证明）

(2)、如图 $2$ ，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B + ∠ D = 180 °$ ， $E 、 F$ 分别是边 $B C 、 C D$ 上的点，且 $∠ E A F = \frac{1}{2} ∠ B A D$ ，（ $1$ ）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

(3)、如图 $3$ ，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B + ∠ D = 180 °$ ， $E 、 F$ 分别是边 $B C 、 C D$ 延长线上的点，且 $∠ E A F = \frac{1}{2} ∠ B A D$ ，（ $1$ ）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

查看试题解析