四川省成都市2023-2024学年七年级上学期期中数学试卷

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（每题4分，共32分）

1. ﹣4的倒数（）

A、4 B、﹣4 C、 $\frac{1}{4}$ D、﹣ $\frac{1}{4}$

查看试题解析
2. 党的十八大以来，以习近平同志为核心的党中央重视技能人才的培育与发展．据报道，截至2021年底，我国高技能人才超过65000000人，将数据65000000用科学记数法表示为（）

A、6.5×10⁶ B、65×10⁶ C、0.65×10⁸ D、6.5×10⁷

查看试题解析
3. 比较（﹣4）³和﹣4³ ，下列说法正确的是（）

A、它们底数相同，指数也相同 B、它们底数相同，但指数不相同 C、它们底数不同，运算结果也不同 D、它们所表示的意义不相同，但运算结果相同

查看试题解析
4. 在代数式﹣7，m，x³y² ， $\frac{1}{a}$ ， 2x+3y中，整式有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 单项式 $- \frac{π x^{3} y^{2}}{5}$ 的系数与次数分别是（）

A、 $- \frac{1}{5}$ ，5 B、 $- \frac{π}{5}$ ，4 C、 $- \frac{1}{5}$ ，6 D、 $- \frac{π}{5}$ ，5

查看试题解析
6. 某商品原价每件x元，后来店主将每件增加10元，再降价25%，则现在的单价（元）是（）

A、25%x+10 B、（1﹣25%）x+10 C、25%（x+10） D、（1﹣25%）（x+10）

查看试题解析
7. 已知|a+b+2|+|b﹣3|＝0，则a﹣2b的值是（）

A、﹣5 B、11 C、5 D、﹣11

查看试题解析
8. 用火柴棒按下图中的方式搭图形如图所示：照这样的规律摆下去，搭第10个图形需要火柴棒的根数为（）

A、50 B、51 C、40 D、41

查看试题解析

二、填空题（每题4分，共20分）

9. 若m+1与﹣4互为相反数，则m的值为．

查看试题解析
10. 如果单项式6x^my²和3x³yⁿ是同类项，则m+n＝．

查看试题解析
11. 设a是最小的正整数，b是绝对值最小的数，c是最大的负整数，则a+b-c= ．

查看试题解析
12. 如图，A，B两点在数轴上（A在B的右侧），点A表示的数是2，AB=6，点C到点A、点B的距离相等，则点C表示的数是．

查看试题解析
13. 下面是数值转换机的示意图．若输入x的值是﹣1，则输出y的值等于．

查看试题解析

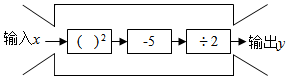
三、解答题（共48分）

14. 计算：

(1)、﹣20﹣（﹣14）+（﹣18）﹣13；

(2)、 $(- \frac{3}{4} + \frac{1}{6} - \frac{5}{8}) \div (- \frac{1}{24})$ ；

(3)、﹣3²+（﹣3）²+3×2+|﹣4|；

(4)、 $16 \div (- 2)^{3} - (- \frac{1}{6}) \times (- 4) + (- 1)^{2024}$ ．

查看试题解析
15. 化简：

(1)、4a³+2b﹣2a³+b；

(2)、2x²+6x﹣6﹣（﹣2x²+4x+1）；

(3)、3（3a²﹣2ab）﹣2（4a²﹣ab）；

(4)、 $6 x y^{2} - [2 x - \frac{1}{2} (2 x - 4 x y^{2}) - x y^{2}]$ ．

查看试题解析
16. 在数轴上表示下列各数，并把这些数按从小到大的顺序用“＜”号连接起来．
﹣（﹣2），0，﹣|﹣1.5|， $\frac{7}{2}$ ， ﹣3.5．

查看试题解析
17. 在抗洪抢险中，解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：+12，-8，+9，-3，+7，-6，+10，-5．

(1)、B地位于A地的什么方向？距离A地多少千米？

(2)、若冲锋舟每千米耗油0.6升，油箱容量为30升，求冲锋舟当天救灾过程中至少还需补充多少升油？

查看试题解析
18. 探究规律，完成相关题目．
定义“*”运算：
（+2）*（+4）＝+（2²+4²）；
（﹣4）*（﹣7）＝[（﹣4）²+（﹣7）²]；
（﹣2）*（+4）＝﹣[（﹣2）²+（+4）²]；
（+5）*（﹣7）＝﹣[（+5）²+（﹣7）²]；
0*（﹣5）＝（﹣5）*0＝（﹣5）²；
0*0＝0²+0²＝0；
（+3）*0＝0*（+3）＝（+3）² ．

(1)、计算：
①（﹣1）*（﹣1）；
②（﹣1）*[0*（﹣2）]；

(2)、归纳*运算的法则（文字语言或符号语言均可）：两数进行*运算时，；特别地，0和任何数进行*运算，或任何数和0进行*运算，；

(3)、是否存在整数m，n，使得（m﹣1）*（n+2）＝﹣2，求出m﹣n的值，若不存在

查看试题解析

四、填空题（每题4分，共20分）

19. 绝对值小于4的所有整数的乘积是．

查看试题解析
20. 当x＝30时，代数式ax³+bx﹣7的值为9，则当x＝﹣30时，代数式ax³+bx+2的值为．

查看试题解析
21. 已知|x|＝2，|y|＝3，则x-y ．

查看试题解析
22. 在数轴上有理数a， $\frac{1}{1 - a}$ 分别用点A，A₁表示，我们称点A₁是点A的“差倒数点”，已知数轴上点A的差倒数点为点A₁ ，点A₁的差倒数点为点A₂；点A₂的差倒数点为点A₃…这样依次得到点A₁ ， A₂ ， A₃ ， …A_n ，若点A，A₁ ， A₂ ， A₃ ， …A_n在数轴上分别表示的有理数为a，a₁ ， a₂ ， a₃ ， …a_n ，则当 $a = \frac{1}{2}$ 时，代数式a₁+a₂+a₃+a₄+⋯+a₂₀₂₃的值为．

查看试题解析
23. |x﹣4|+|x+2|的最小值为； $| \frac{5}{6} x - 1 | + | \frac{1}{2} x - 1 | + | \frac{2}{3} x - 1 |$ = ．

查看试题解析

五、解答题（共30分）

24.

(1)、已知多项式A＝x²+xy+3y，B＝x²﹣xy．
①当x＝﹣2，y＝5时，求2A﹣B的值；
②若2A﹣B的值与y的值无关，求x的值．

(2)、若有理数a、b、c在数轴上的位置如图所示，化简：|a﹣b|+2|a﹣c|﹣|c﹣b|．

查看试题解析
25. 在新冠肺炎防疫工作中，某药店出售酒精与口罩，酒精每瓶定价12元，口罩每个定价6元，药店现开展促销活动，向大家提供两种优惠方案：①买一瓶酒精送一个口罩；②酒精和口罩都按定价的80%付款．小明为班级采购30瓶酒精，x个口罩（x＞30）．

(1)、求小明分别按方案①和方案②购买，需要付的款（用含x的代数式表示）．

(2)、购买多少个口罩时，方案①和方案②费用相同？

(3)、若两种优惠方案可同时使用，当x＝50时，你能给出一种更为省钱的购买方案吗？试写出你的购买方案．

查看试题解析
26. 阅读材料：
已知多项式（a+4）x³+10x²﹣5x+3是关于x的二次多项式，且二次项系数为b，数轴上两点A，B对应的数分别为a，b.

(1)、点A表示的数是，点B表示的数是；

(2)、点A、B同时出发沿数轴向左移动，速度分别为1个单位长度/秒，3个单位长度/秒，经过多少秒，点A与点B相距4个单位？

(3)、点M、N分别从点A、B出发沿数轴向右移动，速度分别为1个单位长度/秒、2个单位长度/秒，点P为ON上靠近点N的三等分点，设OP- $\frac{4}{3}$ AM的值为y，在移动过程中，y值是否发生变化？若不变，求出y值；若变化，说明理由．

查看试题解析