山东省青岛市城阳区2023-2024学年七年级上学期期中数学试卷

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. ﹣ $\frac{1}{8}$ 的倒数是（）

A、8 B、﹣8 C、 $\frac{1}{8}$ D、﹣ $\frac{1}{8}$

查看试题解析
2. 据教育部消息称，2023届全国普通高校毕业生规模预计达1158万，同比增加82万．数据“82万”用科学记数法表示为（　　）

A、8.2×10⁶ B、0.82×10⁵ C、8.2×10⁵ D、82×10⁵

查看试题解析
3. 下列平面图形绕虚线旋转一周，能形成如图这种花瓶形状的几何体的是（　　）

A、 B、 C、 D、

查看试题解析
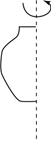4. 检测足球质量，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，如图，下列四个足球中最接近标准质量的是（　　）

A、 B、 C、 D、

查看试题解析
5. 用一个平面去截一个如图的圆柱体，截面不可能是（）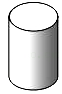

A、 B、 C、 D、

查看试题解析
6. 如图，实数a ， b在数轴上的对应点的位置如图所示，下列结论中正确的是（　　）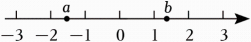

A、a＞b B、|a|＞|b| C、b＜1 D、a＞﹣1

查看试题解析
7. 若单项式﹣a^2﹣^mb²与 $\frac{1}{3} a^{6} b^{n}$ 的和仍是单项式，则mⁿ的值是（　　）

A、3 B、8 C、9 D、16

查看试题解析
8. 下列各式计算正确的是（　　）

A、（2a﹣ab²）﹣（2a+ab²）＝0 B、﹣a²﹣a²＝﹣2a² C、﹣3a²﹣2a²＝﹣5a⁴ D、﹣3xy+（3x﹣2xy）＝3x﹣xy

查看试题解析
9. 将如图折成一个正方体，下列选项的4个点中，与点D重合的是（　　）

A、点A B、点I C、点H D、点F

查看试题解析
10. 如图是由一些相同的小正方体搭成的几何体从三个不同方向看到的形状图，若在所搭几何体的基础上（不改变原几何体中小正方体的位置），继续添加相同的小正方体，搭成一个大正方体，至少还需要小正方体的个数是（　　）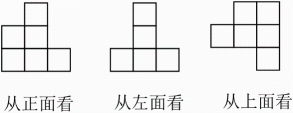

A、9 B、16 C、18 D、27

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 夏天打开冰箱冷冻室门时常常会看到一团“白雾”，这是因为夏天空气温度较高，冰箱内外部温差较大，空气中的水蒸气遇冷凝结成小水滴而形成的．假设夏天空气温度是29°C ，而冰箱冷冻室的温度是﹣18°C ，那么此时的温差是 °C ．

查看试题解析
12. 下列数：﹣（﹣5），（﹣2）³ ， ﹣（﹣1）¹⁰⁰ ， 0， ${(- \frac{1}{6})}^{2}$ ， |﹣0.6|，其中负数有个．

查看试题解析
13. 已知点M在数轴上表示的数是﹣3，点N与点M的距离是4，则点N表示的数是．

查看试题解析
14. 已知一个多项式满足下列条件：①多项式有三项；②多项式的每一项都只含有字母x ， y；③多项式的次数是4次；④多项式的每一项的系数均为1．请写出满足条件的多项式（写出一个即可）．

查看试题解析
15. 如图所示是计算机程序计算，若开始输入x＝﹣1，则最后输出的结果是．

查看试题解析
16. 如图是一组有规律的图案，它们是由大小相同的“ $\times$ ”图案组成的，依此规律，第 $10$ 个图案中有“ $\times$ ”图案个 $.$

查看试题解析

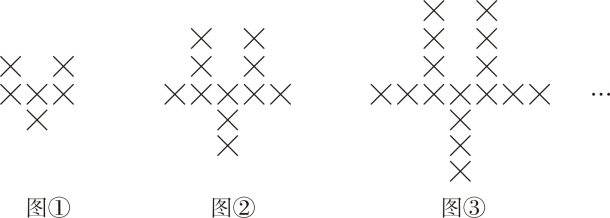
三、作图题（本大题满分3分）

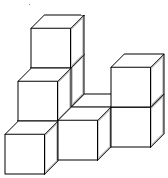
17. 如图是由若干个大小相同的小立方块搭成的几何体，请分别画出从正面、左面、上面所看到的该几何体的形状图．

查看试题解析

四、解答题（本大题共8小题，共69分）

18. 画出数轴，用数轴上的点表示下列各数，并用“＜”将它们连接起来．
$\frac{5}{2}$ ， ﹣3.5，0，3，﹣4， $- 1 \frac{1}{2}$ ．

查看试题解析
19. 计算：

(1)、13+（﹣21）﹣（﹣2）；

(2)、 $(- 0.75) \div \frac{5}{4} \div (- 0.3) - (- \frac{1}{5}) \times 0$ ；

(3)、 $(- \frac{1}{3}) \div {(- \frac{1}{3})}^{2} - 4 \times {(- \frac{1}{2})}^{3}$ ；

(4)、（﹣2²）+3﹣（﹣1）⁴﹣（﹣4）×5；

(5)、 $43 - (\frac{7}{9} - \frac{11}{12} + \frac{1}{6}) \times 36$ ．

查看试题解析
20. 化简：

(1)、（3mn﹣2m²）+（﹣4m²﹣5mn）；

(2)、﹣（2a﹣3b）﹣2（﹣a+5b﹣1）．

查看试题解析
21. 先化简再求值：7x²y﹣2（2x²y﹣3xy²）﹣（4x²y﹣xy²），其中|y﹣1|+（x+2）²＝0．

查看试题解析
22. 如图1是流花河的水文资料（单位：米），取河流的警戒水位作为0点，下表是小明记录的今年雨季流花河一周内水位变化情况（上周末的水位达到警戒水位，正号表示水位比前一天上升，负号表示水位比前一天下降）．
星期
一
二
三
四
五
六
日
水位变化（单位：米）
+0.2
+0.8
﹣0.4
+0.1
+0.3
﹣0.4
﹣0.1
与上周末相比，本周末河流水位是上升了还是下降了？变化了多少？本周末河流水位是多少米？与水文资料中最高水位的距离是多少米？

查看试题解析
23. 如图①，正方形ABCD的边长为a ．

(1)、如图②，延长AB到A₁ ，使A₁B＝BA ，延长BC到B₁ ，使B₁C＝CB ，求四边形B₁A₁AD的面积．

(2)、如图③，延长AB到A₂ ，使A₂B＝b ，延长BC到B₂ ，使B₂C＝b ，求四边形B₂A₂AD的面积．

查看试题解析
24. 将连续奇数1，3，5，7，9………排成如图所示的数表．

(1)、十字框中的五个数字之和与中间数15有什么关系？

(2)、将十字框上下左右移动，可框住另外五个数，设中间数为a ，请你用代数式表示其它四个数，并写出十字框的五个数之和．

(3)、设中间数为a ，十字框中的五个数之和能等于2005吗？说明理由．

查看试题解析
25. 数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．
如图，将一个边长为1的正方形纸片分割成7个部分，部分①是边长为1的正方形纸片面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依次类推．

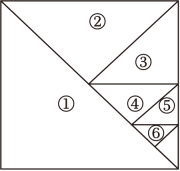(1)、图中阴影部分的面积为；

(2)、受此启发，得到 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ⋯ + \frac{1}{2^{6}}$ ＝；

(3)、联系拓广，得到 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ⋯ + \frac{1}{2^{n}}$ ＝（用含n的式子表示）；

(4)、迁移应用：得到 $\frac{2}{3} + \frac{1}{3} \times \frac{2}{3} + \frac{1}{3^{2}} \times \frac{2}{3} + \frac{1}{3^{3}} \times \frac{2}{3} + ⋯ + \frac{1}{3^{2023}} \times \frac{2}{3}$ ＝（直接写出答案即可）．

查看试题解析

星期	一	二	三	四	五	六	日
水位变化（单位：米）	+0.2	+0.8	﹣0.4	+0.1	+0.3	﹣0.4	﹣0.1