云南省曲靖市麒麟区2023-2024学年九年级上学期第一次随堂检测数学试卷（9月份）

试卷更新日期：2024-01-02 类型：月考试卷

进入出卷网下载

一、选择题(本大题共12个小题，每小题只有一个正确选项，每小题3分，共36分)

1. 下列函数中，y是x的二次函数的是（）

A、y＝ax²+bx+c B、y＝2x C、y＝x+1 D、y＝﹣3x²

查看试题解析
2. 若二次函数y＝ax²的图象经过点P（﹣3，9），则该图象必经过点（）

A、（3，9） B、（﹣3，﹣9） C、（﹣9，3） D、（9，﹣3）

查看试题解析
3. 用配方法解方程x²﹣6x+5＝0，配方后可得（）

A、（x﹣3）²＝5 B、（x﹣3）²＝4 C、（x﹣6）²＝5 D、（x﹣6）²＝31

查看试题解析
4. 如果a是一元二次方程 $2 x^{2} = 6 x - 4$ 的根，则代数式 $a^{2} - 3 a + 2024$ 的值为

A、2021 B、2022 C、2023 D、2024

查看试题解析
5. 对于二次函数 $y = (x - 1)^{2} + 2$ 的图象，下列说法正确的是

A、开口向下 B、对称轴是直线x=-1 C、顶点坐标是（-1，2） D、当 $x < 1$ 时，y随x的增大而减小

查看试题解析
6. 如果关于x的一元二次方程x²+px+q=0的两根分别为x₁=3，x₂=1，那么这个一元二次方程是（）

A、x²+3x+4=0 B、x²﹣4x+3=0 C、x²+4x﹣3=0 D、x²+3x﹣4=0

查看试题解析
7. 把抛物线 $y = 2 (x + 3)^{2} - 5$ 的图象通过怎样平移可以得到抛物线 $y = 2 x^{2}$ 的图象

A、先向上平移3个单位长度，再向右平移5个单位长度 B、先向下平移3个单位长度，再向左平移5个单位长度 C、先向上平移5个单位长度，再向右平移3个单位长度 D、先向上平移3个单位长度，再向左平移3个单位长度

查看试题解析
8. 在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如图所示．如果要使整个挂图的面积是5400cm² ，设金色纸边的宽为xcm，那么x满足的方程是（）

A、x²+65x﹣350＝0 B、x²+130x﹣1400＝0 C、x²﹣65x﹣350＝0 D、x²﹣130x﹣1400＝0

查看试题解析
9. 若关于的一元二次方程 $(k - 1) x^{2} + 2 x - 2 = 0$ 有两个不相等的实数根，则k的取值范围是

A、 $k > \frac{1}{2}$ 且 $k \neq 1$ B、 $k > \frac{1}{2}$ C、 $k ⩾ \frac{1}{2}$ 且 $k \neq 1$ D、 $k ⩾ \frac{1}{2}$

查看试题解析
10. 二次函数y＝ax²+bx+c（a≠0）与一次函数y＝ax+c在同一坐标系中的图象大致为（）

A、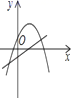 B、 C、 D、

查看试题解析
11. 若点 $A (- 4 ， y_{1}) ， B (- 1 ， y_{2}) ， C (1 ， y_{3})$ 都是二次函数 $y = x^{2} + 4 x + 1$ 的图象上的点，则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
12. 二次函数y＝ax²+bx+c的图象如图所示，给出下列结论：
①abc＞0；②2a+b＜0；③若﹣1＜m＜n＜1，则m+n＜﹣ $\frac{b}{a}$ ；④a+b+c＞0．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共4个小题，每小题2分，共8分）

13. 方程x²+3x=0的根是．

查看试题解析
14. 已知二次函数 $y = x^{2} - 2 x + k$ 的部分图象如图所示，若关于x的一元二次方程 $x^{2} - 2 x + k = 0$ 的一个解为 $x_{1} = 3$ ，则另一个解x₂= ．

查看试题解析
15. 一件商品的原价是300元，连续两次降价后，现售价是243元，若每次降价的百分率相同，那么这个百分率为．

查看试题解析
16. 若抛物线y＝x²﹣2x+m²﹣1的顶点在x轴上，则m的值是．

查看试题解析

三、解答题（本大题共8个小题,共56分）

17. 解方程：

(1)、 $x^{2} - 4 x - 6 = 0$ ；

(2)、 $3 x (2 x + 3) = 4 x + 6$ ．

查看试题解析
18. 关于x的方程x²﹣（m+2）x+（2m﹣1）＝0

(1)、若此方程的一个根为1，求m的值；

(2)、求证：方程恒有两个不相等的实数根．

查看试题解析
19. 已知二次函数y＝x²﹣4x+3．

(1)、将一般式转化为顶点式；

(2)、直接写出该二次函数图象的对称轴和顶点坐标；

(3)、求抛物线与x轴的交点，并直接写出y＜0，x的取值范围．

查看试题解析
20. 已知抛物线y＝（k﹣1）x²﹣2kx+3k，其中k为实数．

(1)、若抛物线经过点（1，3），求k的值；

(2)、若抛物线经过点（1，a），（3，b），试说明ab＞﹣3．

查看试题解析
21. 超市购进一批20元/千克的绿色食品，如果以30元/千克销售，那么每天可售出400千克．由销售经验知，每天销售量y（千克）与销售单价x（元）（x≥30）存在如图所示的一次函数关系式．

(1)、试求出y与x的函数关系式；

(2)、设超市销售该绿色食品每天获得利润P元，当销售单价为何值时，每天可获得最大利润？最大利润是多少？

查看试题解析
22. 某扶贫单位为了提高贫困户的经济收入，购买了33m的铁栅栏，准备用这些铁栅栏为贫困户靠墙（墙长15m围建一个中间带有铁栅栏的矩形养鸡场（如图所示）．

(1)、若要建的矩形养鸡场面积为90cm，求鸡场的长 $(A B)$ 和宽 $(B C)$ ；

(2)、该扶贫单位想要建一个100m²的矩形养鸡场，这一想法能实现吗？请说明理由．

查看试题解析
23. 如图，某隧道口的横截面是抛物线型，已知隧道底部宽AB为10m，最高点离地面的距离OC为5m，以AB的中点O为坐标原点，AB所在直线为x轴，OC所在的直线为y轴，1m为数轴的单位长度，建立平面直角坐标系．

(1)、求抛物线的函数表达式；

(2)、在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度为3m，求两排灯之间的水平距离．

查看试题解析
24. 二次函数图象的顶点在原点O，经过点A（1， $\frac{1}{4}$ ）；点F（0，1）在y轴上，直线y＝﹣1与y轴交于点H．

(1)、求二次函数的解析式；

(2)、点P是抛物线上的点，过点P作x轴的垂线与直线y＝﹣1交于点M，求证：PF＝PM；

(3)、当△FPM是等边三角形时，求P点的坐标．

查看试题解析