四川省绵阳市江油市2023-2024学年九年级上学期期中数学试卷
试卷更新日期:2024-01-02 类型:期中考试
一、选择题:(每小题3分,共36分,每小题给出四个答案中,只有一个符合题目要求,请把你认为正确的题号填入题后面的括号内)
-
1. 将方程x2+5x=7化为一元二次方程的一般形式,其中二次项系数为1,则一次项系数、常数项分别为( )A、5,﹣7 B、5,7 C、﹣5,7 D、﹣5,﹣72. 下列函数中,是二次函数的有( )
①;
②;
③y=3x(1﹣3x);
④y=(1﹣2x)(1+2x).
A、1个 B、2个 C、3个 D、4个3. 用数学的眼光观察下列图形,是中心对称图形的是( )A、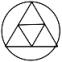 B、
B、 C、
C、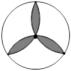 D、
D、 4. 用绳子围成周长为10(m)的矩形,记矩形的一边长为x(m),面积为S(m2).当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )A、一次函数关系 B、二次函数关系 C、反比例函数关系 D、正比例函数关系5. 用配方法解一元二次方程3x2+6x﹣1=0时,将它化为(x+a)2=b的形式,则a+b的值为( )A、 B、 C、2 D、6. 小王同学在求一元二次方程﹣2x2+4x+1=0的近似根时,先在平面直角坐标系中作出了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小王同学的这种方法运用的主要数学思想是( )
4. 用绳子围成周长为10(m)的矩形,记矩形的一边长为x(m),面积为S(m2).当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )A、一次函数关系 B、二次函数关系 C、反比例函数关系 D、正比例函数关系5. 用配方法解一元二次方程3x2+6x﹣1=0时,将它化为(x+a)2=b的形式,则a+b的值为( )A、 B、 C、2 D、6. 小王同学在求一元二次方程﹣2x2+4x+1=0的近似根时,先在平面直角坐标系中作出了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小王同学的这种方法运用的主要数学思想是( )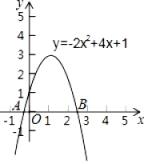 A、数形结合思想 B、类比思想 C、公理化思想 D、模型思想7. 若方程(m﹣1)x|m|+1﹣2x=3是关于x的一元二次方程,则m的值为( )A、1 B、﹣1 C、±1 D、不存在8. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、3(x﹣1)x=6210 B、3(x﹣1)=6210 C、(3x﹣1)x=6210 D、3x=62109. 将抛物线y=2x2向上平移1个单位,再向右平移2个单位,则平移后的抛物线为( )A、y=2(x+2)2+1 B、y=2(x﹣2)2+1 C、y=2(x+2)2﹣1 D、y=2(x﹣2)2﹣110. 如图:已知点A的坐标为 , 菱形ABCD的对角线交于坐标原点O , 则C点的坐标是( )
A、数形结合思想 B、类比思想 C、公理化思想 D、模型思想7. 若方程(m﹣1)x|m|+1﹣2x=3是关于x的一元二次方程,则m的值为( )A、1 B、﹣1 C、±1 D、不存在8. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、3(x﹣1)x=6210 B、3(x﹣1)=6210 C、(3x﹣1)x=6210 D、3x=62109. 将抛物线y=2x2向上平移1个单位,再向右平移2个单位,则平移后的抛物线为( )A、y=2(x+2)2+1 B、y=2(x﹣2)2+1 C、y=2(x+2)2﹣1 D、y=2(x﹣2)2﹣110. 如图:已知点A的坐标为 , 菱形ABCD的对角线交于坐标原点O , 则C点的坐标是( ) A、 B、 C、 D、(﹣2,﹣2)11. 代数式4x2+y2﹣2y﹣4x+15的最小值是( )A、15 B、9 C、13 D、1012. 关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b , 则t的取值范围是( )A、<t< B、﹣1<t≤ C、﹣≤t< D、﹣1<t<
A、 B、 C、 D、(﹣2,﹣2)11. 代数式4x2+y2﹣2y﹣4x+15的最小值是( )A、15 B、9 C、13 D、1012. 关于x的一元二次方程ax2+bx+=0有一个根是﹣1,若二次函数y=ax2+bx+的图象的顶点在第一象限,设t=2a+b , 则t的取值范围是( )A、<t< B、﹣1<t≤ C、﹣≤t< D、﹣1<t<二、填空题:(本大题共6个小题,每小题3分,共18分.将答案直接填写在题中横线上)。
-
13. 在平面直角坐标系中,点P(3m﹣1,2﹣m)与点P′关于原点对称,且点P′在第三象限,则m的取值范围是 .14. 国旗上的每一个五角星是旋转对称图形,它至少需要旋转°后才能与自身重合.15. 若m , n是一元二次方程x2+2022x﹣2023=0的两个实数根,则= .16. 若函数y=ax2﹣x+1(a为常数)的图象与x轴只有一个交点,那么那么a的值是 .17. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.进馆人次的月平均增长率是 .18. 如图,已知△ABC , ∠ABC<60°,将△ABC绕点A逆时针旋转60°得到△ADE , DE与BC交于点P . 下列结论:
①∠EPC=60°;
②AC与DE互相平分;
③PA+PC=PE;
④PA平分∠BPE , 其中正确结论的是 .

三、解答题:(本大题共6个小题,共46分.解答应写出文字说明、证明过程或推理步骤。)
-
19.(1)、解方程:x2﹣2x﹣24=0.(2)、△ABC和点S在平面直角坐标系中的位置如图所示.
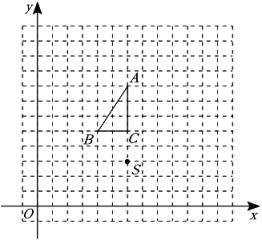
①将△ABC向右平移4个单位得到△A1B1C1 , 画出平移后的图形;
②将△ABC绕点S按顺时针方向旋转90°,画出旋转后的图形.
20.(1)、已知二次函数y=x2﹣2x﹣3,求:①抛物线与x轴、y轴相交的交点坐标.
②抛物线的顶点坐标.
③画出此抛物线的图象,利用图象回答问题:当x取何值时,函数值大于0?
(2)、已知关于x的一元二次方程x2+3x+k﹣2=0有实数根.①求实数k的取值范围.
②设方程的两个实数根分别为x1 , x2 , 若(x1+1)(x2+1)=﹣1,求k的值.
21. 一个凸多边形共有20条对角线,它是几边形?是否存在有18条对角线的多边形?如果存在,它是几边形?如果不存在,说明得出结论的道理.22. 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.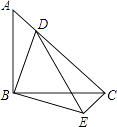 (1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.23. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.
(1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.23. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.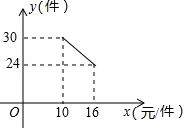 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图,在平面直角坐标系xOy中,一次函数的图象与x轴交于点A , 与y轴交于点B , 点C的坐标为(﹣2,0),抛物线经过A , B , C三点.
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图,在平面直角坐标系xOy中,一次函数的图象与x轴交于点A , 与y轴交于点B , 点C的坐标为(﹣2,0),抛物线经过A , B , C三点.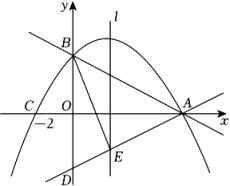 (1)、求抛物线的解析式;(2)、直线AD与y轴负半轴交于点D , 且∠BAO=∠DAO , 求证:OB=OD;(3)、在问题2的条件下,若直线AD与抛物线的对称轴l交于点E , 连接BE , 在平面内是否存在一点P , 使以B . E . A . P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、直线AD与y轴负半轴交于点D , 且∠BAO=∠DAO , 求证:OB=OD;(3)、在问题2的条件下,若直线AD与抛物线的对称轴l交于点E , 连接BE , 在平面内是否存在一点P , 使以B . E . A . P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.