湖南省长沙市雅礼集团2023-2024学年九年级上学期期中数学试题

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. 3的相反数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、 $- 3$

查看试题解析
2. 下面用数学家名字命名的图形中，既是轴对称图形，又是中心对称图形的是（）

A、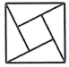赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 下列各运算中，正确的运算是（）

A、 $(2 a)^{3} = 8 a^{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $a^{8} \div a^{4} = a^{2}$ D、 $(a - b)^{2} = a^{2} - b^{2}$

查看试题解析
4. 今年是共建“一带一路”倡议提出10周年。十年来，作为“一带一路”重要节点城市，长沙实现了内陆腹地到开放前沿的“华丽蜕变”。据海关统计，2022年，长沙与“一带一路”共建国家进出口贸易额为175000000000元．数据175000000000用科学记数法表示为（）

A、 $17.5 \times 1 0^{10}$ B、 $1.75 \times 1 0^{11}$ C、 $0.175 \times 1 0^{12}$ D、 $1.75 \times 1 0^{10}$

查看试题解析
5. 下列说法中，正确的是（）

A、检测“神舟十六号”载人飞船零件的质量，应采用抽样调查 B、甲、乙两组数据的方差分别是 $s_{甲}^{2} = 0.4$ ， $s_{乙}^{2} = 2$ ，则乙组数据比甲组数据稳定 C、“任意画一个三角形，其内角和是 $18 0^{°}$ ”是必然事件 D、从2000名学生中随机抽取100名学生进行调查，样本容量为2000名学生

查看试题解析
6. 在函数 $y = \sqrt{x - 1}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \geq 1$ B、 $x > 1$ C、 $x \leq 1$ D、 $x < 1$

查看试题解析
7. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如表所示．
成绩米
1.50
1.60
1.65
1.70
1.75
人数
2
3
5
4
1
这些运动员成绩的众数和中位数分别为（）

A、1.65米，1.70米 B、1.65米，1.65米 C、1.75米，1.65米 D、1.50米，1.60米

查看试题解析
8. 二次函数 $y = a x^{2} + b x - 1 (a \neq 0)$ 的图象经过点 $(1 ， 1)$ ，则 $a + b + 1$ 的值是（）

A、3 B、 $- 1$ C、2 D、 $- 3$

查看试题解析
9. 如图，点 $A$ ， $B$ ， $C$ 在 $⊙ O$ 上，连结 $A B$ ， $A C$ ， $O B$ ， $O C$ ．若 $∠ B A C = 50 °$ ，则 $∠ B O C =$ （）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、 $110 °$

查看试题解析
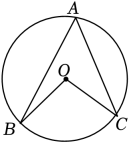10. 伴随2023城市自然行动——“1864大熊猫巡展”在长沙站的正式启动，湖南省地质博物馆迅速成了巡展的热门打卡地.某学校九年级学生去距学校 $10 k m$ 的湖南省地质博物馆参观，一部分学生骑自行车先走，过了 $20 m i n$ 后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．若设骑车学生的速度为 $x$ $k m / h$ ，则可列方程为（）

A、 $\frac{10}{2 x} - \frac{10}{x} = 20$ B、 $\frac{10}{x} - \frac{10}{2 x} = 20$ C、 $\frac{10}{2 x} - \frac{10}{x} = \frac{1}{3}$ D、 $\frac{10}{x} - \frac{10}{2 x} = \frac{1}{3}$

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 分解因式： $x^{2} - 4 =$

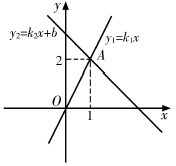
查看试题解析
12. 在平面直角坐标系中，点 $M (1 ， 2)$ 关于原点对称的点的坐标是．

查看试题解析
13. 已知圆锥的母线长为4，底面圆的半径为3，该圆锥的侧面展开图的面积为．

查看试题解析
14. 如图，直线y₁=k₁x与直线y₂=k₂x+b交于点A（1，2）．当y₁<y₂时，x的取值范围是．

查看试题解析
15. 若关于 $x$ 的方程 $x^{2} + m x - 6 = 0$ 的一个根为1，则 $m =$ ．

查看试题解析
16. 我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术：“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率 $π$ 的近似值为3.1416．如图， $⊙ O$ 的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计 $⊙ O$ 的面积，可得 $π$ 的估计值为 $\frac{3 \sqrt{3}}{2}$ ，若用圆内接正十二边形作近似估计，可得 $π$ 的估计值为．

查看试题解析

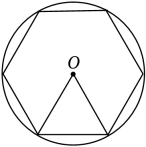
三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21 题每小题8分，第22、23题每小题9分，第24、25题每小题10分，共72分，解答写出必要的文字说明、证明过程或演算步骤）

17. 计算： $(3.14 - π)^{0} + | \sqrt{2} - 1 | + (\frac{1}{2})^{- 1} - \sqrt{8}$ ．

查看试题解析
18. 先化简，再求值： $(a + 3)^{2} + (a + 3) (a - 3) - 2 a (3 - a)$ ，其中 $a = - \frac{1}{2}$ ．

查看试题解析
19. 如图，网格中每个小正方形的边长均为1，线段 $O A$ 的端点均在小正方形的格点上．

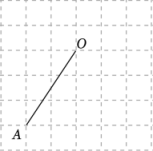(1)、画出线段 $O A$ 绕点 $O$ 顺时针旋转 $90 °$ 后得到的线段 $O B$ ；

(2)、在（1）的运动过程中，请计算出点 $A$ 绕点 $O$ 旋转到点 $B$ 所经过的路径长（结果保留 $π)$ ．

查看试题解析
20. “强国必须强语，强语助力强国。”为全面落实国家语言文字方针政策，弘扬中华民族优秀传统文化，某学校组织学生参加了“推广普通话，奋进新征程”为主题的朗诵比赛．该校随机抽取部分学生比赛成绩进行统计，将成绩分为四个等级： $A$ （优秀）， $B$ （良好）， $C$ （一般）， $D$ （不合格），并根据结果绘制成如图所示的两幅不完整的统计图．
根据图中所给信息解答下列问题：

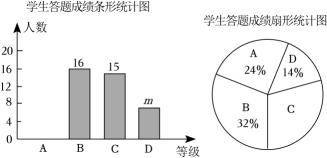(1)、这次调查活动共抽取人；

(2)、条形统计图中的 $m =$ ▲ ；“ $C$ ”等所在扇形的圆心角的度数为度；

(3)、请将条形统计图补充完整（要求在条形图上方表明人数）；

(4)、学校要从答题成绩为 $A$ 等且表达能力较强的甲、乙、丙、丁四名学生中，随机抽出两名学生去做“推广普通话宣传员”，请用列表或画树状图的方法，求抽出的两名学生恰好是甲和乙的概率．

查看试题解析
21. 如图，矩形 $A B C D$ 中，过对角线 $B D$ 的中点 $O$ 作 $B D$ 的垂线 $E F$ ，分别交 $A D$ ， $B C$ 于点 $E$ ， $F$ ，连接 $B E$ 、 $D F$ .

(1)、求证： $Δ B O F$ ≌ $Δ D O E$ ；

(2)、若 $A B = 4 ， A D = 8 ，$ 求四边形 $E B F D$ 的周长．

查看试题解析
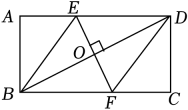22. “健康湖南，云动潇湘”，为迎接2023年全民健身线上运动会，某中学计划购进一批篮球和排球.若购买3个篮球和1个排球共需360元；若购买5个篮球和3个排球共需680元．

(1)、求每个篮球和每个排球的价格分别是多少元？

(2)、该学校计划购进篮球和排球共100个，且购买篮球的个数不少于排球个数的3倍，怎样购买才能使总费用最少？并求出最少总费用.

查看试题解析
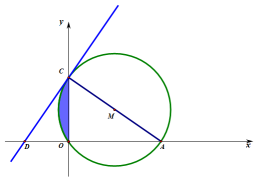23. 如图，在平面直角坐标系中， $⊙ M$ 经过原点 $O (0 ， 0)$ ，点 $A (2 \sqrt{3} ， 0)$ 与点 $C (0 ， 2)$ ，点 $D$ 在 $x$ 轴负半轴上，连接 $C D$ ，且 $∠ D C O = ∠ O A C$ .

(1)、求 $⊙ M$ 的半径；

(2)、求证：直线 $C D$ 为 $⊙ M$ 的切线；

(3)、求图中阴影部分的面积.（结果保留 $π$ 和根号）．

查看试题解析
24. 我们约定：若一次函数的图象与二次函数的图象有两个交点，并且都在坐标轴上，则称二次函数和一次函数互为“息息相关”函数，这两个交点称为两个函数的“相关点”．根据约定，解答下列问题：

(1)、判断函数 $y = 2 x + 1$ 与 $y = 2 x_{}^{2} + 3 x + 1$ 是否是互为“息息相关”函数，如果是，求出其“相关点”．

(2)、函数y=x+3c（c为常数且 $c > 0)$ 的图象与 $x$ 轴交于点 $A$ ，其“息息相关”函数y=ax²+2bx+3c与 $x$ 轴的另一交点为点 $B$ ，若 $O A = 3 O B$ ，求 $b$ 的值．

(3)、若函数 $y_{1}^{} = x + 1$ 的“息息相关”函数为 $y_{2}^{} = m x_{}^{2} + n x + t$ ，使函数 $y = y_{2}^{} - y_{1}^{} - m$ 在 $m \leq x \leq m + 1$ 时的最小值为 $m$ ，求函数 $y$ 的解析式．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点 $A (2 ， 0)$ ，和点 $B (4 ， 0)$ ，直线是对称轴．

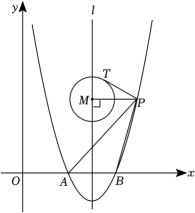(1)、求该抛物线的函数表达式；

(2)、在直线上是否存在点 $C$ ，使 $∠ A C B = 4 5^{°}$ ？若存在，求出点 $C$ 的坐标；若不存在，请说明理由.

(3)、 $P$ 为第一象限内抛物线上的一个动点，且在直线右侧，连接 $P A$ ， $P B$ ，过点 $P$ 作 $P M ⊥ l$ ，垂足为 $M$ ，以点 $M$ 为圆心，作半径为 $r$ 的圆， $P T$ 与 $⊙ M$ 相切，切点为 $T$ ．若 $P T^{2} = S_{Δ P A B}$ ，且 $⊙ M$ 不经过点 $(3 ， 3)$ ，求 $P M$ 长的取值范围．

查看试题解析

成绩米	1.50	1.60	1.65	1.70	1.75
人数	2	3	5	4	1