湖南省怀化市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2024-01-02 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 已知点在双曲线上,则下列各点中,在此双曲线上的点是( )A、 B、 C、 D、2. 下列方程中是一元二次方程的是( )A、 B、 C、 D、3. 用配方法解方程 , 配方正确的是( )A、 B、 C、 D、4. 如图,在中, , , 若 , 则等于( )
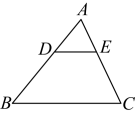 A、5 B、4 C、 D、25. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、6. 杭州亚运会吉祥物深受大家喜爱.某商户8月份销售吉祥物“宸宸”摆件10万个,10月份销售万个.设该摆件销售量的月平均增长率为x,则可列方程为( )A、 B、 C、 D、7. 如图,在中, . 将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A、
A、5 B、4 C、 D、25. 若点都在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、6. 杭州亚运会吉祥物深受大家喜爱.某商户8月份销售吉祥物“宸宸”摆件10万个,10月份销售万个.设该摆件销售量的月平均增长率为x,则可列方程为( )A、 B、 C、 D、7. 如图,在中, . 将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A、 B、
B、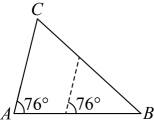 C、
C、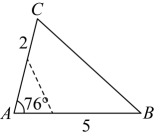 D、
D、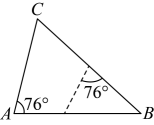 8. 定义:一元二次方程()若满足 , 那么我们称这个方程为“和谐”方程,若满足 , 那么我们称这个方程为“友善”方程.已知关于的方程()既是“和谐”方程,又是“友善”方程,则下列结论中正确的是( )A、方程有两个相等的实数根 B、方程的两个根互为相反数 C、两根之积为0 D、无实数根9. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
8. 定义:一元二次方程()若满足 , 那么我们称这个方程为“和谐”方程,若满足 , 那么我们称这个方程为“友善”方程.已知关于的方程()既是“和谐”方程,又是“友善”方程,则下列结论中正确的是( )A、方程有两个相等的实数根 B、方程的两个根互为相反数 C、两根之积为0 D、无实数根9. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )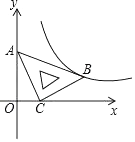 A、( ,0) B、(2,0) C、( ,0) D、(3,0)10. 如图,在中, , , . 点是边上一动点,过点作交于点 , 为线段的中点,当平分时,的长度为( )
A、( ,0) B、(2,0) C、( ,0) D、(3,0)10. 如图,在中, , , . 点是边上一动点,过点作交于点 , 为线段的中点,当平分时,的长度为( )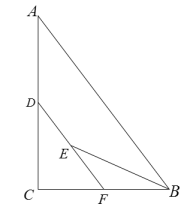 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
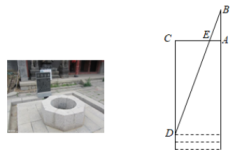
11. 反比例函数的图象分布在第一、三象限内,则的取值范围为 .12. 若m是方程的一个根,则代数式 .13. 设 ,那么 .14. 已知点P是线段的黄金分割点, , 若 , 则的值为15. 已知一菱形的两条对角线长分别是方程x2-9x+20=0的两根,则菱形的面积是 .16. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 , 从木杆的顶端B观察井水水岸D,视线与井口的直径交于点E,如果测得米,米,米,那么为米.
 17. 若关于x的一元二次方程的常数项为0.则m的值等于 .18. 如图,点是反比例函数上一点,矩形的周长是 , 正方形和正方形的面积之和为 , 则反比例函数的解析式是 .
17. 若关于x的一元二次方程的常数项为0.则m的值等于 .18. 如图,点是反比例函数上一点,矩形的周长是 , 正方形和正方形的面积之和为 , 则反比例函数的解析式是 .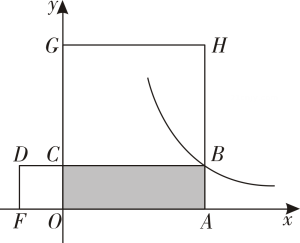
三、解答题(8小题,共66分)
-
19. 解下列方程:(1)、(2)、20. 如图,平面直角坐标系中,的顶点都在正方形网格的格点上.
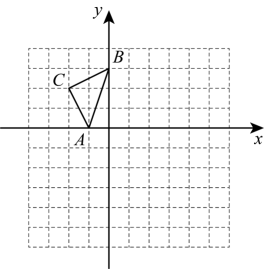 (1)、以O点为位似中心,位似比的绝对值为2,将放大为 , 请在网格图中画出(只画出其中一种);(2)、若 , 的面积分别为S、 , 写出S、的数量关系.21. 如图,在正方形中,点M、N分别在上, , , .
(1)、以O点为位似中心,位似比的绝对值为2,将放大为 , 请在网格图中画出(只画出其中一种);(2)、若 , 的面积分别为S、 , 写出S、的数量关系.21. 如图,在正方形中,点M、N分别在上, , , .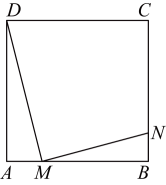 (1)、求证:;(2)、与有什么数量关系,请说明理由;(3)、与有什么位置关系,请说明理由.22. 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点B处时,李明直立时身高的影子恰好是线段 , 并测得 , 已知李明直立时的身高为 , 求路灯的高的长.(结果精确到.
(1)、求证:;(2)、与有什么数量关系,请说明理由;(3)、与有什么位置关系,请说明理由.22. 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点B处时,李明直立时身高的影子恰好是线段 , 并测得 , 已知李明直立时的身高为 , 求路灯的高的长.(结果精确到.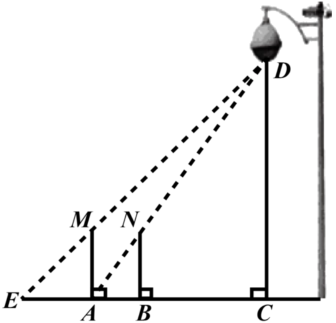 23. 已知关于x的方程 .(1)、当m满足什么条件时,方程有实数根?(2)、设方程的两实根分别为、 , 且 , 求m的值.24. 直福购物逐渐走进了人们的生活,某电商在料者上对一款成本价为40元的小商品进行直播销售、如果按每件60元销售,每天可卖出20件,通过市场调查发现,每件小商品的售价每降低1元,则日销售量可增加2件.(1)、当每件小商品的售价为50元时,日销售量为件;(2)、若计划每日获利448元,为了尽快减少库存,每件售价应定为多少元?
23. 已知关于x的方程 .(1)、当m满足什么条件时,方程有实数根?(2)、设方程的两实根分别为、 , 且 , 求m的值.24. 直福购物逐渐走进了人们的生活,某电商在料者上对一款成本价为40元的小商品进行直播销售、如果按每件60元销售,每天可卖出20件,通过市场调查发现,每件小商品的售价每降低1元,则日销售量可增加2件.(1)、当每件小商品的售价为50元时,日销售量为件;(2)、若计划每日获利448元,为了尽快减少库存,每件售价应定为多少元?

