湖南省长沙市浏阳市2023-2024学年九年级上学期期中数学试题

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分．在各小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡上指定的位置填符合要求的选项字母代号．）

1. 方程 $5 x^{2} - 1 = 4 x$ 的二次项系数和一次项系数分别为（）

A、5和4 B、5和 $- 4$ C、5和 $- 1$ D、5和1

查看试题解析
2. 下面四种交通标志图中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x + 2)}^{2} = 9$ C、 ${(x - 1)}^{2} = 6$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
4. 已知 $x = 1$ 是方程 $x^{2} + k x + 4 = 0$ 的一个根，则方程的另一个根为（）

A、 $- 1$ B、4 C、5 D、 $- 4$

查看试题解析
5. 抛物线 $y = - 3 x^{2} - x + 4$ 与x轴的交点个数是（）

A、3 B、2 C、1 D、0

查看试题解析
6. 若二次函数 $y = {(x - 1)}^{2} - 1$ 的图象如图所示，则坐标原点可能是（）

A、点A B、点B C、点C D、点D

查看试题解析
7. 如图，在一块长为 $22 m$ ，宽为 $17 m$ 的矩形地面内（两条道路分别与矩形的一条边平行），余下的铺上草坪，要使草坪的面积达到 $300 m^{2}$ ，设道路的宽为 $x m$ ，可列方程为（）

A、 $17 \times 22 - 17 x - 22 x = 300$ B、 $(22 - x) (17 - x) + x^{2} = 300$ C、 $(22 - x) (17 - x) = 300$ D、 $2 (22 - x + 17 - x) = 300$

查看试题解析
8. 已知 $P (3 ， 4)$ ，将P绕坐标原点顺时针旋转 $90 °$ 后得到 $P_{1}$ ，则 $P_{1}$ 的坐标为（）

A、 $(- 3 ， 4)$ B、 $(4 ， 3)$ C、 $(4 ， - 3)$ D、 $(3 ， - 4)$

查看试题解析
9. 如图，P是正三角形 $A B C$ 内的一点，且 $P A = 6$ ， $P B = 8$ ， $P C = 10$ ．若将 $△ P A C$ 绕点A逆时针旋转后，得到 $△ M A B$ ，则 $∠ A P B$ 等于（）．

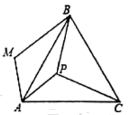A、120° B、135° C、150° D、160°

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象如图．下列结论：① $a b c > 0$ ；② $a - b + c < 0$ ；③若m为任意实数，则有 $a + b \geq a m^{2} + b m$ ；④若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x_{2}$ ，且 $x_{1} \neq x_{2}$ _，则 $x_{1} + x_{2} = 2$ ；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6题，每小题3分，共18分，只需要将结果直接填写在答题卡对应题号处的横线上，不必写出解答过程，不填、错填，一律得0分）

11. 请写出一个常数c的值，使得关于x的方程 $x^{2} + 2 x + c = 0$ 无实数根，则c的值可以是．

查看试题解析
12. 二次函数 $y = - 3 x^{2} - 6$ 的最大值是．

查看试题解析
13. 二次函数 $y = - (x + 1)^{2} - 2$ 与 $y$ 轴的交点坐标是．

查看试题解析
14. 将抛物线 $y = - 2 x^{2} + 3$ 向右平移 $1$ 个单位，再向上平移 $2$ 个单位，所得抛物线的函数表达式是．

查看试题解析
15. 在研究二次函数 $y = - {(x + 1)}^{2} - 3$ 的图象和性质时，甲、乙、丙、丁四位同学的说法如下：甲：图象的顶点坐标为 $(- 1 ， - 3)$ ；乙：函数的图象关于直线 $x = - 1$ 对称；丙：当 $x = 1$ 时，函数取得最大值 $- 3$ ；丁：当 $x < - 1$ 时， $y$ 随 $x$ 的增大而增大．其中，说法错误的是同学．

查看试题解析
16. 如图，四边形 $A B C D$ 中的两条对角线 $A C$ ， $B D$ 互相垂直， $A C + B D = 10$ ，当 $A C$ 为时．四边形 $A B C D$ 的面积最大．

查看试题解析

三、解答题（要求写出必要的解题步骤）

17. 解方程：2(x－3)＝3x(x－3)．

查看试题解析
18. 如图： $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 40 °$ ，将 $R t △ A B C$ 绕点C顺时针旋转一个角度后，点D正好落在 $A B$ 上，求 $∠ A C E$ ．

查看试题解析
19. 参加足球联赛的每两队之间都进行两场比赛．共要比赛90场．共有多少个队参加比赛？

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} + 2 m x + m^{2} + m = 0$ 有实数根.

(1)、求 $m$ 的取值范围；

(2)、若该方程的两个实数根分别为 $x_{1}$ 、 $x_{2}$ ，且 $x_{1}^{2} + x_{2}^{2} = 12$ ，求 $m$ 的值.

查看试题解析
21. 为满足广大群众阅读需求，浏阳图书馆不断完善藏书数量，今月7月份图书馆中有藏书50000册，到今月9月份其中藏书数量增长到72000册．

(1)、求浏阳图书馆这两个月藏书的平均增长率．

(2)、按照这样的增长方式，请你估算出今月10月份浏阳图书馆的藏书量是多少？

查看试题解析
22. 如图，顶点为M的抛物线y＝a（x+1）²﹣4分别与x轴相交于点A，B（点A在点B的右侧），与y轴相交于点C（0，﹣3）．

(1)、求抛物线的函数表达式；

(2)、判断△BCM是否为直角三角形，并说明理由．

查看试题解析
23. 在国庆期间，大润发商场新上市了一款童装，进价每件 $80$ 元，现以每件 $120$ 元销售，每天可售出 $20$ 件．在试销售阶段发现，若每件童装降价 $1$ 元，那么每天就可多售 $2$ 件，设每件童装单价降价了 $x$ 元．

(1)、若销售单价降低 $5$ 元，则该款童装每天的销售量为件，每天利润是元；

(2)、请写出每天销售该款童装的利润 $y$ （元）与每件童装降价 $x$ （元）之间的函数关系式；

(3)、当每件童装销售单价定为多少元时，商场每天可获得最大利润？最大利润是多少元？

查看试题解析
24. 我们不妨定义：如果两个图形（或函数图象）关于y轴对称，我们称互为蝴蝶图形（或互为蝴蝶图像）；如果两个图形（或函数图象）关于x轴对称，我们称互为倒影图形（或互为倒影图像）；如果两个图形（或函数图象）关于原点对称，我们称互为梦幻图形（或互为梦幻函数图象）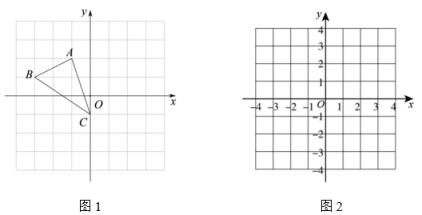

(1)、在图1中画出 $△ A B C$ 的蝴蝶图形．

(2)、直接写出图像 $y = x + 1$ 的倒影图像的解析式：

(3)、已知函数图象m是函数图象 $y = x^{2} - 2 x - 3$ 的梦幻函数图象，则函数图象m的解析式为 ▲ （要求顶点式），并列表描点法在图2画出函数图象，利用函数图象m直接写出当 $- 3 < x < 0$ ， y的取值范围 ▲ ．
列表
x
…

…
y
…

…

查看试题解析
25. 如图，点 $A (0 ， - 2)$ ， B为x轴上一动点，线段AB的垂直平分线CD交y轴于点D， $B C ⊥ x$ 轴交CD于C，记 $C (m ， n)$ ．

(1)、点C的轨迹是
①一条直线；②一条关于y轴对称的折线；③一条抛物线；

(2)、求n与m的关系式；

(3)、在B的运动过程中，是否存在 $△ A B C$ 是等边三角形，如果不存在请说明理由，如果存在请求出此时C的坐标；

(4)、当点O到直线CD距离等于2时，直接写出 $m^{2}$ 的值．

查看试题解析

x	…						…
y	…						…