江西省吉安市十校联盟2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-02 类型:期中考试
一、选择题(本大题共6小题,每小题3分,共18分)
-
1. 在实数 , , , 3.14中,无理数是( )A、 B、 C、 D、3.142. 下列各组数分別为一个三角形三边的长,其中能构成直角三角形的一组是( )A、1,2,3 B、4,5,6 C、7,24,25 D、8,15,183. 如图,是象棋盘的一部分,若“帅”位于点 , “相”位于点上,则“炮”位于点( )上.
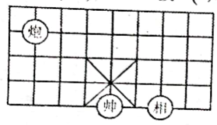 A、 B、 C、 D、4. 如图,数轴上,点为线段BC的中点, , 两点对应的实数分别是和 , 则点所对应的实数是( )
A、 B、 C、 D、4. 如图,数轴上,点为线段BC的中点, , 两点对应的实数分别是和 , 则点所对应的实数是( ) A、 B、 C、 D、5. 在平面直角坐标系中,一次函数的图象的随的增大而减小,且 , 则它的图象大致是( )A、
A、 B、 C、 D、5. 在平面直角坐标系中,一次函数的图象的随的增大而减小,且 , 则它的图象大致是( )A、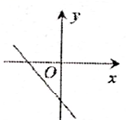 B、
B、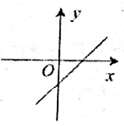 C、
C、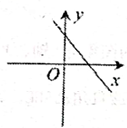 D、
D、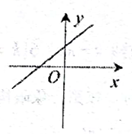 6. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , ……,按这样的运动规律,经过第2025次运动后,动点的坐标是( ).
6. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , ……,按这样的运动规律,经过第2025次运动后,动点的坐标是( ).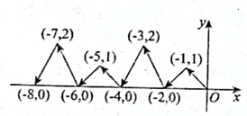 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6个小题,每小题3分,共18分)
-
7. 点 关于 轴的对称点坐标为 .8. 函数中自变量的取值范围是 .9. 程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,根据如图的程序进行计算,当输入们值为64时,输出的值是 .
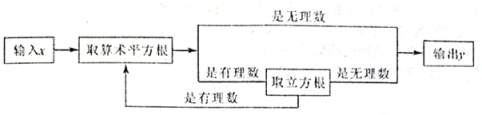 10. 若直线下移后经过点(5,1),则平移后的直线解析式为 .11. 如图,将两个大小、形状完全相同的和拼在一起,其中点与点重合,点落在边AB上,连接 . 若 , , 则的长度为 .
10. 若直线下移后经过点(5,1),则平移后的直线解析式为 .11. 如图,将两个大小、形状完全相同的和拼在一起,其中点与点重合,点落在边AB上,连接 . 若 , , 则的长度为 . 12. 在平面直角坐标系中,长方形按如图所示放疽,是AD的中点,且、、的坐标分别为 , , , 点是BC上的动点,当是腰长为5的等腰三角形时,则点的坐标为 .
12. 在平面直角坐标系中,长方形按如图所示放疽,是AD的中点,且、、的坐标分别为 , , , 点是BC上的动点,当是腰长为5的等腰三角形时,则点的坐标为 .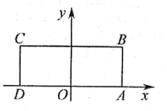
三、解答题(本大题共5小题,每小题各6分,共30分)
-
13. 计算:(1)、 .(2)、 .14. 已知正数的两个不同的平方根分别是和 , 求的立方根.15. 如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫做格点.
图1
 图2
图2 (1)、在图1中以格点为顶点画一个面积为10的正方形:(2)、在图2中以格点为顶点画一个三角形,使三解形三边长分别为2, , .16. 在第十四届全国人大一次会议召开之际,某中学举行了庄严的升旗仪式.看着着再升起的五星红旗(如图1),小乐想用刚学过的知识计算旗杆的高度.如图2,AD为旗杆AE上用来固定国旗的绳子,点D距地面的高度 . 将绳子AD拉至AB的位置,测得点到AE的距离 , 到地面的垂直高度 , 求旗杆AE的高度.
(1)、在图1中以格点为顶点画一个面积为10的正方形:(2)、在图2中以格点为顶点画一个三角形,使三解形三边长分别为2, , .16. 在第十四届全国人大一次会议召开之际,某中学举行了庄严的升旗仪式.看着着再升起的五星红旗(如图1),小乐想用刚学过的知识计算旗杆的高度.如图2,AD为旗杆AE上用来固定国旗的绳子,点D距地面的高度 . 将绳子AD拉至AB的位置,测得点到AE的距离 , 到地面的垂直高度 , 求旗杆AE的高度.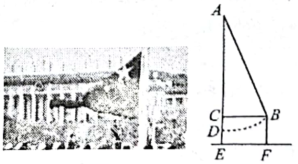
图1 图2
17. 某城市居民用水实行阶梯收费,每户每月用水量如果未超过5吨,每吨收费2元;超过5吨时,超过的部分每吨收费3.5元,设某户每月用水量为吨,应收水费为元.(1)、写出每月用水量超过5吨时,与之间的函数关系式:(2)、若某户居民某月交水费17元,该户居民用水多少吨?四、(本大题共3小题,每小题各8分,共24分)
-
18. 已知,如图,Rt中, , , , 以斜边AC为底边作等腰三角形ACD,腰AD刚好满足 , 并作腰上的高AE.
 (1)、求证:AB=AE;(2)、求等腰三角形的腰长CD.19. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
(1)、求证:AB=AE;(2)、求等腰三角形的腰长CD.19. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , . (1)、若和关于轴成轴对称,画出 , 点的坐标为 ▲ ;(2)、在轴上求作一点 , 使得的值最小,请在图中画出点:(3)、求的面积和最长边上的高.20. 如图,在平面直角坐标系, , , , 且与互为相反数.
(1)、若和关于轴成轴对称,画出 , 点的坐标为 ▲ ;(2)、在轴上求作一点 , 使得的值最小,请在图中画出点:(3)、求的面积和最长边上的高.20. 如图,在平面直角坐标系, , , , 且与互为相反数. (1)、求实数与的值;(2)、在轴的正半轴上存在一点 , 使 , 请通过计算求出点的坐标;(3)、在坐标轴的其他位詛是否存在点 , 使仍然成立?若存在,请直接写出符合题意的点的坐标.
(1)、求实数与的值;(2)、在轴的正半轴上存在一点 , 使 , 请通过计算求出点的坐标;(3)、在坐标轴的其他位詛是否存在点 , 使仍然成立?若存在,请直接写出符合题意的点的坐标.五、(本大题共2小题,每小题9分,共18分)
-
21. 先观察下列的计算,再完成:(1)、计算:;(2)、观察上面的解题过程,请直接写出的结果为;(3)、根据你的猜想、归纳,运用规律计算:
求的值
22. 在一条直线上依次有、、三个港口,甲、乙两船同时分别从、港口出发,沿直线匀速驶向C港,最终到达C港停止.设甲、乙两船行驶后,与港的距离分别为、 , 、与的关系则图所示.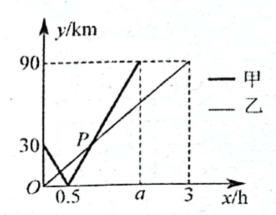 (1)、B、C两港口间的距离为 , ;(2)、甲船出发几小时追上乙船?(3)、在整个过程中,什么时候甲乙两船相距?
(1)、B、C两港口间的距离为 , ;(2)、甲船出发几小时追上乙船?(3)、在整个过程中,什么时候甲乙两船相距?六、解答题(本大题共1小题,共12分)
-
23. 【探索发现】如图1,等腰直角三角形ABC中, , , 直线DE经过点 , 过作于点 . 过作于点 , 则 , 我们称这种全等模型为“型全等”.(不需要证明)
【迁移应用】已知:直线的图象与轴、轴分别交于A、B两点.
图1
 图2
图2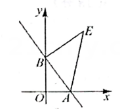 图3
图3 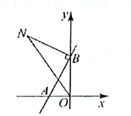 图4
图4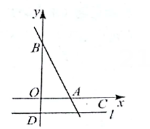 (1)、如图2,当时,在第一象限构造等腰直角 , ;直接写出 , ;(2)、如图3,当的取值变化,点随之在轴负半轴上运动时,在轴左侧过点B作 , 并且 , 连接ON,问的面积是否发生变化?若不变,求出其值;若变,请说明理由;(3)、【拓展应用】如图4,当时,直线与轴交于点 , 点、分别是直线和直线AB上的动点,点在轴上们坐标为 , 当是以CQ为斜边的等腰直角三角形时,点的坐标是 .
(1)、如图2,当时,在第一象限构造等腰直角 , ;直接写出 , ;(2)、如图3,当的取值变化,点随之在轴负半轴上运动时,在轴左侧过点B作 , 并且 , 连接ON,问的面积是否发生变化?若不变,求出其值;若变,请说明理由;(3)、【拓展应用】如图4,当时,直线与轴交于点 , 点、分别是直线和直线AB上的动点,点在轴上们坐标为 , 当是以CQ为斜边的等腰直角三角形时,点的坐标是 .