江西省赣州市章贡区2023-2024学年九年级上学期期中数学试题
试卷更新日期:2024-01-02 类型:期中考试
一、单项选择题(本大题6小题,每小题3分,共18分)
-
1. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、2. 我国古代数学的许多创新与发明都曾在世界上有深远影响.下列图形“杨辉三角”,“赵爽弦图”,“中国七巧板”,“刘微割圆术”中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若是一元二次方程的一个根,则方程的另一个根及m的值分别是( )A、0, B、0,0 C、 , D、2,24. 在正方形网格中有 , 绕O点按逆时针旋转90°后的图案应该是( )A、
3. 若是一元二次方程的一个根,则方程的另一个根及m的值分别是( )A、0, B、0,0 C、 , D、2,24. 在正方形网格中有 , 绕O点按逆时针旋转90°后的图案应该是( )A、 B、
B、 C、
C、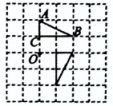 D、
D、 5. 如图,是的内接三角形,且AB是的直径,点P为上的动点,且 , 的半径为6,则点P到AC距离的最大值是( )
5. 如图,是的内接三角形,且AB是的直径,点P为上的动点,且 , 的半径为6,则点P到AC距离的最大值是( ) A、6 B、12 C、 D、6. 二次函数(a , b , c为常数,且)中的x与y的部分对应值如下表:
A、6 B、12 C、 D、6. 二次函数(a , b , c为常数,且)中的x与y的部分对应值如下表:x
0
1
3
y
3
5
3
下列结论:①;②当时,y的值随x值的增大而减小;③3是方程的一个根;④当时,.其中正确结论的个数是( )
A、4 B、3 C、2 D、1二、填空题(本大题6小题,每小题3分,共18分)
-
7. 关于x的一元二次方程有实数根,则k的取值范围是.8. 抛物线与x轴只有一个公共点,则c的值为.9. 如图,在中,弦AB , CD相交于点P.若 , , 则的度数是.
 10. 已知、是一元二次方程的两个根,则的值为.11. 如图,平面直角坐标系中有两个二次函数的图象,其顶点P , Q皆在x轴上,且有一水平线与两图象相交于A、B、C、D四点,各点位置如图所示,若 , , , 则PQ的长度为.
10. 已知、是一元二次方程的两个根,则的值为.11. 如图,平面直角坐标系中有两个二次函数的图象,其顶点P , Q皆在x轴上,且有一水平线与两图象相交于A、B、C、D四点,各点位置如图所示,若 , , , 则PQ的长度为. 12. 已知抛物线 , M是抛物线上一动点,以点M为圆心,1个单位长度为半径作.当与x轴相切时,点M的坐标为.
12. 已知抛物线 , M是抛物线上一动点,以点M为圆心,1个单位长度为半径作.当与x轴相切时,点M的坐标为.三、解答题(本大题共5小题,每小题6分,共30分)
-
13.(1)、解方程:(2)、如图,在中,AB , AC为互相垂直且相等的两条弦, , , 垂足分别为D , E.
求证:四边形ADOE为正方形,
 14. 如图,和都是等边三角形,且B、C、D三点共线.
14. 如图,和都是等边三角形,且B、C、D三点共线. (1)、可以看作是由△绕着点 , 逆时针旋转°得到;(2)、试证明这两个三角形全等.15. 某广场要建一个圆形喷水池,计划在池中心位置O竖直安装一根顶部A带有喷水头的水管,如图,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心的水平距离也为3m,那么水管OA的高度应为多少?
(1)、可以看作是由△绕着点 , 逆时针旋转°得到;(2)、试证明这两个三角形全等.15. 某广场要建一个圆形喷水池,计划在池中心位置O竖直安装一根顶部A带有喷水头的水管,如图,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心的水平距离也为3m,那么水管OA的高度应为多少? 16. 如图,点A , B在上,点O是的圆心,请你仅用无刻度的直尺,在图1和图2中分别画出以点B为顶点,与互余的圆周角(保留作图痕迹)
16. 如图,点A , B在上,点O是的圆心,请你仅用无刻度的直尺,在图1和图2中分别画出以点B为顶点,与互余的圆周角(保留作图痕迹)图1
 图2
图2 (1)、图1中,点C在上;(2)、图2中,点C在内.17. 随着我国经济的强劲复苏,外出旅游的人越来越多.某景区游容人数逐月增加、2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
(1)、图1中,点C在上;(2)、图2中,点C在内.17. 随着我国经济的强劲复苏,外出旅游的人越来越多.某景区游容人数逐月增加、2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?四、解答题(本大题共3小题,每小题8分,共24分)
-
18. 已知关于x的一元二次方程(1)、求证:无论m为何值,方程总有实数根;(2)、若 , 是方程的两个实数根,且 , 求m的值.19. 如图1,已知是的内接三角形,AB为直径, , D为上一点.
图1
 图2
图2 (1)、当点D为的中点时,连接DB , DC , 求和的大小;(2)、如图2,过点D作的切线,与AB的延长线交于点P , 且 , 连接DC , OC , 求的大小.20. 如图1,在平面直角坐标系中,抛物线经过点和点.
(1)、当点D为的中点时,连接DB , DC , 求和的大小;(2)、如图2,过点D作的切线,与AB的延长线交于点P , 且 , 连接DC , OC , 求的大小.20. 如图1,在平面直角坐标系中,抛物线经过点和点.图1
 图2
图2  图3
图3 (1)、求抛物线的表达式;(2)、如图2,抛物线与抛物线关于原点O成中心对称,请直接写出抛物线的表达式为;(3)、如图3,将(2)中抛物线向上平移m个单位,得到抛物线 , 当抛物线经过点A时,求m的值.
(1)、求抛物线的表达式;(2)、如图2,抛物线与抛物线关于原点O成中心对称,请直接写出抛物线的表达式为;(3)、如图3,将(2)中抛物线向上平移m个单位,得到抛物线 , 当抛物线经过点A时,求m的值.五、解答题(本大题共2小题,每小题9分,共18分)
-
21. 为加强劳动教育,落实五育并举.某中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位:元)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元.
 (1)、当时,元;(2)、设2023年甲乙两种蔬菜种植总成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降.若甲种蔬菜种植成本平均每年下降10%,乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的种植总成本为28920元?22. 如图1,已知AB是的直径,且 , BM切于点B , 点P是上的一个动点(不经过A , B两点),连接PA , 过点O作交BM于点Q , 过点P作于点C , 交QO的延长线于点E , 连接AE , PQ.
(1)、当时,元;(2)、设2023年甲乙两种蔬菜种植总成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降.若甲种蔬菜种植成本平均每年下降10%,乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的种植总成本为28920元?22. 如图1,已知AB是的直径,且 , BM切于点B , 点P是上的一个动点(不经过A , B两点),连接PA , 过点O作交BM于点Q , 过点P作于点C , 交QO的延长线于点E , 连接AE , PQ.图1
 (备用图)
(备用图) (1)、求证:;(2)、试判断PQ与的位置关系,并给予证明;(3)、随着点P的移动,四边形PAEO能否为菱形,若能,请说明点E与的位置关系,并求出PE的长;若不能,请说明理由.
(1)、求证:;(2)、试判断PQ与的位置关系,并给予证明;(3)、随着点P的移动,四边形PAEO能否为菱形,若能,请说明点E与的位置关系,并求出PE的长;若不能,请说明理由.六、解答题(本大题共12分)
-
23. 已知二次函数(1)、以下有关二次函数L的性质结论序号正确的有.(填序号)
①二次函数的开口向上;
②二次函数的对称轴是直线;
③二次函数的图象经过定点和;
④函数值y随着x的增大而减小.
(2)、若二次函数的图象关于点中心对称得到二次函数G的图象,则称这两个二次函数关于点成对称抛物线.
①求抛物线G的表达式(用含m的式子表示):
②若抛物线G的顶点纵坐标y与横坐标x之间存在一个函数关系式H , 求出这个函数关系式;若二次函数L与函数H的图象有交点,请结合图象求出m的取值范围.