四川省泸州市龙马潭区 2023-2024学年九年级上学期10月月考数学试题
试卷更新日期:2024-01-02 类型:月考试卷
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的).
-
1. 下列方程是关于x的一元二次方程的是( )A、ax2+bx+c=0 B、 + =2 C、x2+2x=y2-1 D、3(x+1)2=2(x+1)2. 函数y=3(x-1)2+2的图象的顶点坐标是 ( )A、(1,-4) B、(-1,2) C、(1,2) D、(0,3)3. 如果2是方程x2-3x+k=0的一个根,那么常数k的值为( )A、1 B、2 C、-1 D、-24. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=a(x+c)2的图象大致为( )A、
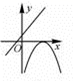 B、
B、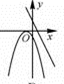 C、
C、 D、
D、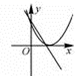 5. 方程x2+6x=5的左边配成完全平方式后所得方程为( )A、(x+3)2=14 B、(x-3)2=14 C、(x+6)2=12 D、以上答案都不对6. 将抛物线y=3x2平移得到抛物线y=3(x-4)2-1 的步骤是( )A、向左平移4个单位,再向上平移1个单位 B、向左平移4个单位,再向下平移1个单位 C、向右平移4个单位,再向上平移1个单位 D、向右平移4个单位,再向下平移1个单位7. 一元二次方程x2+3x+5=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断8. (﹣4,y1),(2,y2)与(3,y3)为二次函数y=2x2﹣4x+5图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y1<y2 D、y2<y1<y39. 二次函数图象上部分点的坐标对应值列表如下:
5. 方程x2+6x=5的左边配成完全平方式后所得方程为( )A、(x+3)2=14 B、(x-3)2=14 C、(x+6)2=12 D、以上答案都不对6. 将抛物线y=3x2平移得到抛物线y=3(x-4)2-1 的步骤是( )A、向左平移4个单位,再向上平移1个单位 B、向左平移4个单位,再向下平移1个单位 C、向右平移4个单位,再向上平移1个单位 D、向右平移4个单位,再向下平移1个单位7. 一元二次方程x2+3x+5=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断8. (﹣4,y1),(2,y2)与(3,y3)为二次函数y=2x2﹣4x+5图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y1<y2 D、y2<y1<y39. 二次函数图象上部分点的坐标对应值列表如下:x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的对称轴是( )
A、x=﹣3 B、x=﹣2 C、x=﹣1 D、x=010. 关于x的方程(k+1)x2-2x+1=0有实数根,则k的取值范围是( )A、k<0 B、k≤0 C、k<0且k≠-1 D、k≤0且k≠-111. 已知三角形的两边长为4和5,第三边的长是方程x2-5x+6=0的一个根,则这个三角形的周长是( )A、11 B、12 C、11或12 D、1512. 已知关于x的二次函数y=(x-m)2-3,当x>2时,y随着x的增大而增大,则m的取值范围是( )A、m≤2 B、m≥-2 C、m<2 D、m≤-2二、填空题(本大题共4个小题,每小题3分,共12分).
-
13. 方程的解是 .14. 二次函数 的图象与y轴的交点坐标是 .15. 已知a,b是一元二次方程x2-6x+4=0的两个根,则=16. 关于x的二次函数y=ax2 -4ax+b中,当1≤x≤4时,-3≤y≤5. 则b-4a的值为
三、本大题共3个小题,每小题6分,共18分.
-
17. 计算:18. 用适当的方法解方程:3x2+2x-5=0.19. 先化简再求值:(a+1﹣)÷ , 其中a是方程x2+2x﹣3=0的根.
四、本大题共2个小题,每小题7分,共14分.
-
20. 雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.如果第二天、第三天收到捐款的增长率相同,求捐款增长率;21. 若抛物线的顶点坐标是A(-1,-3),并且抛物线经过点B坐标为(1,-1).(1)、求出该抛物线的关系式;(2)、当x满足什么条件时,y随x的增大而增大
五、本大题共2个小题,每小题8分,共16分.
-
22. 已知关于x的一元二次方程x2+(2m-1)x+m2-1=0有实数根.(1)、求m的取值范围;(2)、设此方程的两个根分别为x1 , x2 , 若x12+x22=16+x1x2 , 求m的值.23. 如图,已知y=-2x+3的图象与y=x2的图象交于点A,B两点,且与x轴,y轴分别交于点D,C两点,O为坐标原点
 (1)、求点A,B的坐标(2)、求S△AOB的值
(1)、求点A,B的坐标(2)、求S△AOB的值六、本大题共2个小题,每小题12分,共24分.
-
24. 某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.(1)、设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示,最后结果为最简)(2)、每件童装降价多少元时,平均每天赢利1200元.(3)、要想平均每天赢利2000元,可能吗?请说明理由.25. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx+3与x轴交于点A(3,0), B(-1,0).
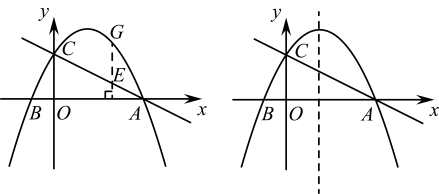 (1)、求抛物线的解析式;(2)、点G为直线AC上方抛物线上一动点,过点G作GE垂直于x轴交AC于点E,当GE最大时,求G点的坐标.(3)、在抛物线是否存在点P,使s△ABP=4,若存在,求出点P坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点G为直线AC上方抛物线上一动点,过点G作GE垂直于x轴交AC于点E,当GE最大时,求G点的坐标.(3)、在抛物线是否存在点P,使s△ABP=4,若存在,求出点P坐标,若不存在,请说明理由.