湖北省武汉市黄陂区2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2024-01-02 类型:期中考试
一、选择题(每小题3分,共30分)本题共10小题,每小题均给出A,B,C,D四个选项,有且只有一个答案是正确的,请将正确答案的代号填在答题卡上,填在试题卷上无效.
-
1. 以下列各组线段为边,能组成三角形的是( ).A、 B、 C、 D、2. 第19届亚运会于2023年9月23日至10月8日在杭州成功举行,中国运动健儿发扬拼搏精神,共获得201金再次金牌榜蝉联第一.下列体育运动图标是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 3. 下列图形中具有稳定性的是( ).A、等边三角形 B、平行四边形 C、正方形 D、正多边形4. 如图,和相交于点 , 则下列结论正确的是( ).
3. 下列图形中具有稳定性的是( ).A、等边三角形 B、平行四边形 C、正方形 D、正多边形4. 如图,和相交于点 , 则下列结论正确的是( ). A、 B、 C、 D、5. 一个三角形的三个内角度数之比为 , 则这个三角形是( ).A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定6. 在中, , 则边上的高的长度是( ).A、5 B、 C、 D、7. 如图,在中,是和角平分线的交点,则的度数为( ).
A、 B、 C、 D、5. 一个三角形的三个内角度数之比为 , 则这个三角形是( ).A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定6. 在中, , 则边上的高的长度是( ).A、5 B、 C、 D、7. 如图,在中,是和角平分线的交点,则的度数为( ).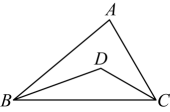 A、 B、 C、 D、8. 阅读以下作图步骤:
A、 B、 C、 D、8. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且9. 如图,在中,平分 , 延长至点 , 使 , 连接 . 若 , 则为( ).
A、且 B、且 C、且 D、且9. 如图,在中,平分 , 延长至点 , 使 , 连接 . 若 , 则为( ).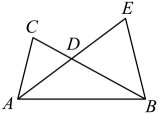 A、12 B、16 C、18 D、2010. 如图,在四边形中, , 点为上的点(不与重合),观察下列图形中全等三角形的对数. 其中,图1中有3对全等三角形,图2中有6对全等三角形,图3中有10对全等三角形,…. 按此规律,第5个图中有( )对全等三角形.
A、12 B、16 C、18 D、2010. 如图,在四边形中, , 点为上的点(不与重合),观察下列图形中全等三角形的对数. 其中,图1中有3对全等三角形,图2中有6对全等三角形,图3中有10对全等三角形,…. 按此规律,第5个图中有( )对全等三角形. A、15 B、16 C、18 D、21
A、15 B、16 C、18 D、21二、填空题(每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
-
11. 已知等腰三角形的一边长为4,一边长为9,则它的周长为 .12. 若n边形的内角和是它的外角和的2倍,则n=.13. 已知三角形的三边分别为 , 那么的取值范围是 .14. 已知是的高, , 则 .15. 如图, , 过点的直线分别交于点 . 下列结论:
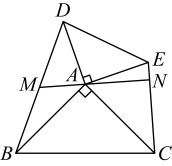
①若为的中点,则;
②若于点 , 则为的中点;
③若为的中点,则;
④ .
其中正确的结论有 . (填写序号即可)
16. 在平面直角坐标系中,为等腰直角三角形, , 若点不在第一象限,符合条件的点的坐标为 .三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
-
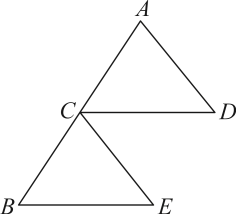
17. 如图,C是AB的中点,AD=CE , CD=BE , 求证△ACD≌△CBE .
 18. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
18. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.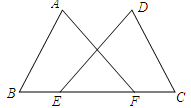 19. 在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求∠C的度数.20. 在中, , 过直角顶点作直线于点于点 .
19. 在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求∠C的度数.20. 在中, , 过直角顶点作直线于点于点 . (1)、如图1,当与边不相交时,判断之间的数量关系,并说明理由;(2)、当与边相交时,请在图2中画出图形,并直接写出之间的数量关系.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点. 的三个顶点都是格点. 仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示.
(1)、如图1,当与边不相交时,判断之间的数量关系,并说明理由;(2)、当与边相交时,请在图2中画出图形,并直接写出之间的数量关系.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点. 的三个顶点都是格点. 仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示.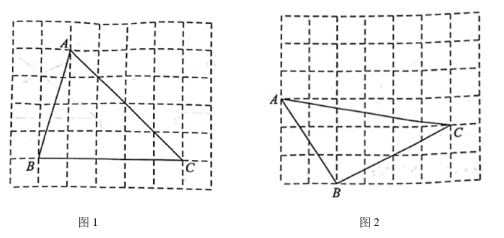 (1)、在图1中,先画 , 且 , 再在上画点 , 使;(2)、在图2中,先画格点 , 使得 , 画出射线 , 再在射线上画点 , 使得 .22.(1)、点关于轴对称的点的坐标是;
(1)、在图1中,先画 , 且 , 再在上画点 , 使;(2)、在图2中,先画格点 , 使得 , 画出射线 , 再在射线上画点 , 使得 .22.(1)、点关于轴对称的点的坐标是;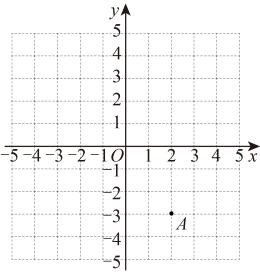 (2)、直线过点 , 且与轴垂直,则点关于直线对称的点的坐标是 , 点关于直线对称的点的坐标是;(3)、若点和点关于直线对称,求的值.
(2)、直线过点 , 且与轴垂直,则点关于直线对称的点的坐标是 , 点关于直线对称的点的坐标是;(3)、若点和点关于直线对称,求的值.