湖南省衡阳市横山县2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、单选题（30分）

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{1.5}$ B、 $\sqrt{45}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{x^{2} + y^{2}}$

查看试题解析
2. 下列图形中−定相似的是（）

A、直角三角形都相似 B、等腰三角形都相似 C、矩形都相似 D、等腰直角三角形都相似

查看试题解析
3. 若关于 $x$ 的一元二次方程 $m x^{2} - 2 x + 1 = 0$ 有实数根，则实数 $m$ 的取值范围是（）

A、 $m \geq 1$ B、 $m \leq 1$ C、 $m \geq 1$ 且 $m \neq 0$ D、 $m \leq 1$ 且 $m \neq 0$

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{25} = \pm 5$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $\sqrt{18} \div \sqrt{2} = 9$ D、 $\sqrt{24} \cdot \sqrt{\frac{3}{2}} = 6$

查看试题解析
5. 方程 $x - 3 = x (x - 3)$ 的解为（）

A、 $x = 0$ B、 $x_{1} = 0$ ， $x_{2} = 3$ C、 $x = 3$ D、 $x_{1} = 1$ ， $x_{2} = 3$

查看试题解析
6. 如图，直线 $A B ∥ C D ∥ E F$ ，若 $A C = 3$ ， $A E = 7$ ，则 $\frac{B D}{D F}$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析
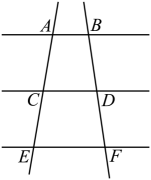7. 某班毕业时，每位同学将自己的照片向全班其他同学各送一张表示留念，全班共送1892张照片，如果全班有x名同学，根据题意，列出方程（）

A、 $x (x + 1) = 1892$ B、 $x (x - 1) = 1892$ C、 $\frac{1}{2} x (x + 1) = 1892$ D、 $\frac{1}{2} x (x - 1) = 1892$

查看试题解析
8. 若0＜ $x$ ＜1，那么 $x + 1 + \sqrt{{(x - 1)}^{2}}$ 的化简结果是（）

A、 $2 x$ B、 $2$ C、 $0$ D、 $2 x + 2$

查看试题解析
9. 如图，在平行四边形 $A B C D$ 中，点 $E$ 在边 $B C$ 上， $B E ： E C = 1 ： 2$ ，连接 $A E$ 交 $B D$ 于点 $F$ ，则 $B F ： F D =$ （　　）

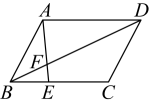A、2：3 B、1：2 C、1：3 D、1：4

查看试题解析
10. 如图，小明晚上由路灯 $A$ 下的点 $B$ 处走到点 $C$ 处时，测得自身影子 $C D$ 的长为1米，他继续往前走3米到达点 $E$ 处，测得自己影子 $E F$ 的长为2米，已知小明的身高是1.5米，那么路灯 $A$ 的高度 $A B$ 是（）

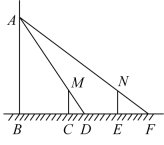A、4.5米 B、6米 C、7.5米 D、8米

查看试题解析

二、填空题（18分）

11. 式子 $\sqrt{2 a + 1}$ 在实数范围内有意义，则实数a的取值范围是．

查看试题解析
12. 若方程 $x^{2} + 2 x - k = 0$ 的一个根是 $0$ ，则另一个根是．

查看试题解析
13. 计算： $\frac{\sqrt{50} - \sqrt{18}}{\sqrt{2}} =$ ．

查看试题解析
14. 如图，要使 $△ A F E ∽ △ A B C$ ，可以添加条件∶ ．

查看试题解析
15. 已知 $a$ 是方程 $x^{2} - 2 x - 1 = 0$ 的一个根，那么代数式 $2 a^{2} - 4 a + 5$ 的值为．

查看试题解析
16. 如图，在平面直角坐标系中，点 $A$ 在函数 $y = - \frac{10}{x} (x < 0)$ 的图象上，点 $B$ 在函数 $y = \frac{k}{x} (x > 0)$ 图象上，若 $O A = 2 O B$ ， $∠ A O B = 90 °$ ，则 $k$ 的值为．

查看试题解析

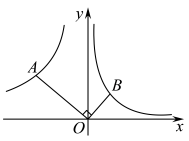
三、解答题

17. 解方程：

(1)、 $x^{2} - 3 x = 0$

(2)、 $x^{2} + 8 x + 1 = 0$ ．

查看试题解析
18. 计算：

(1)、 $\sqrt{{(- 5)}^{2}} - \sqrt[3]{8} + \sqrt{9}$

(2)、 $| \sqrt{2} - \sqrt{3} | + \sqrt{3} (\sqrt{3} - 1) + \sqrt{2}$

查看试题解析
19. 化简求值： ${(x - y)}^{2} - x (x - 2 y)$ ，其中x是 $\sqrt{5}$ 的整数部分，y是 $\sqrt{5}$ 的小数部分．

查看试题解析
20. 如图，在 $△ A B C$ 和 $△ D E C$ 中， $∠ B C E = ∠ A C D$ ， $∠ B = ∠ C E D$ ．

(1)、求证： $△ A B C ∼ △ D E C$ ；

(2)、若 $S_{△ A B C} ： S_{△ D E C} = 4 ： 9$ ， $B C = 12$ ，求 $E C$ 的长．

查看试题解析
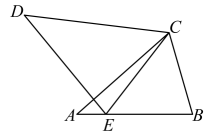21. 已知关于x的一元二次方程 $(x - 3) (x - 2) - p^{2} = 0$ ．

(1)、求证：无论p为何值，方程总有两个不等的实数根；

(2)、若方程的两根 $x_{1} 、 x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} = 15$ ，求p的值．

查看试题解析
22. 阅读材料：如果一个三角形的三边长分别为a ， b ， c ，记 $p = \frac{a + b + c}{2}$ ，那么这个三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ．这个公式叫“海伦公式”，它是利用三角形的三条边的边长直接求三角形面积的公式，中国秦九韶也得出了类似的公式，称三斜求积术，故这个公式又被称为“海伦-秦九韶公式”．完成下列问题：如图，在 $△ A B C$ 中， $a = 8$ ， $b = 5$ ， $c = 7$ ．

(1)、求 $△ A B C$ 的面积；

(2)、过点A作 $A D ⊥ B C$ ，垂足为D、求线段 $A D$ 的长．

查看试题解析
23. 超市以每件25元的进价购进一批商品，当商品售价为40元时，三月份销售256件，四、五月该商品十分畅销，销售量持续上涨，在售价不变的基础上，五月份的销售量达到400件．

(1)、求四、五这两个月销售量的月平均增长百分率．

(2)、经市场预测，六月份的销售量将与五月份持平，现商场为了减少库存，采用降价促销方式，经调查发现，该商品每降价1元，月销量增加5件，当商品降价多少元时，商场六月份可获利4250元？

查看试题解析
24. 如图，在平面直角坐标系中，A、B两点的坐标分别为（20，0）和（0，15），动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动，动直线EF从x轴开始以每秒1cm的速度向上平行移动（即EF∥x轴），分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．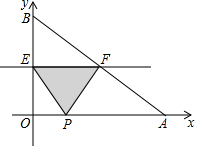

(1)、求t=9时，△PEF的面积；

(2)、直线EF、点P在运动过程中，是否存在这样的t使得△PEF的面积等于40cm²？若存在，请求出此时t的值；若不存在，请说明理由；

(3)、当t为何值时，△EOP与△BOA相似．

查看试题解析
25. 我们知道求函数图象的交点坐标，可以联立两个函数解析式组成方程组，方程组的解就是交点的坐标．如：求直线 $y = 2 x + 3$ 与 $y = - x + 6$ 的交点坐标，我们可以联立两个解析式得到方程组 ${\begin{array}{l} y = 2 x + 3 \\ y = - x + 6 \end{array}$ ，解得 ${\begin{array}{l} x = 1 \\ y = 5 \end{array}$ ，所以直线 $y = 2 x + 3$ 与 $y = - x + 6$ 的交点坐标为 $(1 ， 5)$ ．请利用上述知识解决下列问题：

(1)、求直线 $y = x - 2$ 和双曲线 $y = \frac{3}{x}$ 的交点坐标；

(2)、已知直线 $y = k x - 3$ 和抛物线 $y = x^{2} + 2 x + 4$ ，若直线与抛物线只有一个交点，则 $k$ 的值为；

(3)、如图已知点 $A (a ， 0)$ 是x轴上的动点， $B (0 ， 4 \sqrt{2})$ ，以AB为边在AB右侧作正方形ABCD ，当正方形ABCD的边与反比例函数 $y = \frac{2 \sqrt{2}}{x}$ 的图像有4个交点时，请直接求出a的取值范围．

查看试题解析