湖南省永州市宁远县2023-2024学年七年级上学期数学期中考试试卷
试卷更新日期:2024-01-02 类型:期中考试
一、选择题(每题3分,共36分,将答案填在表格内)
-
1. 用科学记数法表示的数 , 它原来是( )位数A、10 B、11 C、12 D、132. 观桌子上有7只杯口朝上的茶杯,每次翻转3只,经过n次翻转可使这7只杯子的杯口全部朝下,则n的最小值为( )A、2 B、3 C、4 D、53. 如图,半径为2个单位长度的半圆,从原点沿数轴向右滚动一周,则点所对应的数是( )
 A、 B、 C、 D、4. “算24点”的游戏规则是:用“ , , , ”…四种运算符号把给出的4个数字连接起来进行计算,要求最终算出的结果是24,例如,给出2,2,2,8这四个数, 可以列式 . 以下的4个数用“ , , , ”四种运算符号不能算出结果为24的是( )A、1,6,8,7 B、1,2,3,4 C、4,4,10,10 D、6,3,3,85. 如果规定汽车向东行驶5千米记作千米,那么向西行驶10千米记作( )A、千米 B、千米 C、千米 D、千米6. 取一个整数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明.但举例验证都是正确的.例如:取自然数5.经过下面5步运算可得1,即:如图所示.如果自然数m恰好经过8步运算可得到1,则所有符合条件的m的值有( )
A、 B、 C、 D、4. “算24点”的游戏规则是:用“ , , , ”…四种运算符号把给出的4个数字连接起来进行计算,要求最终算出的结果是24,例如,给出2,2,2,8这四个数, 可以列式 . 以下的4个数用“ , , , ”四种运算符号不能算出结果为24的是( )A、1,6,8,7 B、1,2,3,4 C、4,4,10,10 D、6,3,3,85. 如果规定汽车向东行驶5千米记作千米,那么向西行驶10千米记作( )A、千米 B、千米 C、千米 D、千米6. 取一个整数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明.但举例验证都是正确的.例如:取自然数5.经过下面5步运算可得1,即:如图所示.如果自然数m恰好经过8步运算可得到1,则所有符合条件的m的值有( )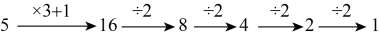 A、3个 B、4个 C、5个 D、6个7. 已知 , 则代数式 的值是( )A、-101 B、101 C、99 D、-998. 下列方程是一元一次方程的是( )A、 B、 C、 D、9. 已知 , 根据等式性质变形为 , 那么 , 必须符合的条件是( )A、 B、 C、 D、 , 为任意有理数或式子10. 要使多项式化简后不含的二次项,则等于( )A、0 B、1 C、 D、11. 若a为一位数,b为两位数,把a置于b的左边,则所得的三位数可表示为( )A、 B、 C、 D、12. 已知数的大小关系如图,下列说法:①;②;③;④若为数轴上任意一点,则的最小值为 . 其中正确结论的个数是( )
A、3个 B、4个 C、5个 D、6个7. 已知 , 则代数式 的值是( )A、-101 B、101 C、99 D、-998. 下列方程是一元一次方程的是( )A、 B、 C、 D、9. 已知 , 根据等式性质变形为 , 那么 , 必须符合的条件是( )A、 B、 C、 D、 , 为任意有理数或式子10. 要使多项式化简后不含的二次项,则等于( )A、0 B、1 C、 D、11. 若a为一位数,b为两位数,把a置于b的左边,则所得的三位数可表示为( )A、 B、 C、 D、12. 已知数的大小关系如图,下列说法:①;②;③;④若为数轴上任意一点,则的最小值为 . 其中正确结论的个数是( )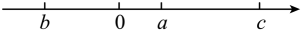 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每题3分,共24分)
-
13. 如果a是有理数,那么的最小值是 .14. 已知:|x|=3,|y|=2,且xy<0,则x+y的值为等于.15. 若单项式x2ym与xny3的和仍是单项式,则m+n= .16. 若表示m , n两数中较小的数,则的值为 .17. 定义一种新运算,其运算规则是 , 那么 .18. 已知a , b为常数,且三个单项式 , , 相加得到的和仍然是单项式,那么 .19. 猜数字游戏中,小明写出如下一组数: , , , , , …,小亮猜测出第六个数是 , 根据此规律,第n(n为正整数)个数是 .20. 若关于的方程是一元一次方程,则 .
三、解答题(共60分)
-
21.(1)、;(2)、22. 先去括号,再合并同类项.(1)、(2)、23.(1)、当时,求两个代数式与的值;(2)、当时,再求以上两个代数式的值;(3)、你能从上面的计算结果中,发现上面有什么结论?
结论是:
24. 出租车司机小张某天下午的营运可以看作全是在东西走向的大道上行驶的,若规定向东为正,行车记录情况(单位,千米)如下: .(1)、当把最后一名乘客送到目的地时,小张在出发地的哪个方向?距离为多少?(2)、小张的平均营运额为元/千米,成本为 元/千米,求这天下午小张盈利多少元.25. 有理数a、b、c在数轴上的位置如图,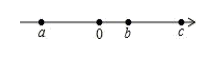 (1)、用“>”或“<”填空:0,0, 0;(2)、化简: .26. 如图,数轴上点表示的数为 , 点表示的数为 , 为原点,且 , 表示的数满足 .
(1)、用“>”或“<”填空:0,0, 0;(2)、化简: .26. 如图,数轴上点表示的数为 , 点表示的数为 , 为原点,且 , 表示的数满足 .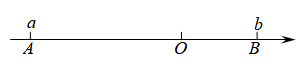 (1)、 , ;(2)、若点、分别以个单位长度/秒和个单位长度/秒的速度沿数轴向右运动,两点同时移动.
(1)、 , ;(2)、若点、分别以个单位长度/秒和个单位长度/秒的速度沿数轴向右运动,两点同时移动.①当点运动到对应的点时,求、两点间的距离;
②经过多长时间、两点相距个单位长度?
27. 大数学家高斯在上学读书时曾经研究过这样一个问题:经过研究,这个问题的结论是 , (n是正整数).现在我们来研究一个类似的问题:
观察下面三个特殊的等式,并且填空:
,
,
,
① ▲ ,…
将前两个等式的两边相加,可以得到 .
将三个等式的两边相加,可以得 .
根据以上知识完成填空:
②计算: ▲ ;
③计算: ▲ ;
④计算: ▲ ;
⑤依据上面的材料,试计算:;
⑥猜想: ▲ .