湖南省永州市宁远县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2024-01-02 类型:期中考试
一、选择题
-
1. 若反比例函数的图象一定经过的点是( )A、 B、 C、 D、2. 下列属于一元二次方程的是( )A、 B、 C、 D、3. 已知 , , , 成比例线段,其中 , , , 则( )A、8cm B、9.5cm C、4cm D、4.5cm4. 下列说法正确的有个( )
任意两个矩形都相似 任意两个正方形都相似
任意两个等边三角形都相似 任意两个菱形都相似.
A、0 B、1 C、2 D、35. 下列一元二次方程中,没有实数根的是( )A、 B、 C、. D、6. 如图,在平面直角坐标系中,的顶点C , A分别在x轴,y轴上, , , 且斜边轴.若反比例函数的图象恰好经过的中点D , 则k的值为( ) A、 B、 C、 D、7. 某班毕业时,每位同学将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程( )A、 B、 C、 D、8. 在同一直角坐标系中,函数与的图象可能是( )A、
A、 B、 C、 D、7. 某班毕业时,每位同学将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程( )A、 B、 C、 D、8. 在同一直角坐标系中,函数与的图象可能是( )A、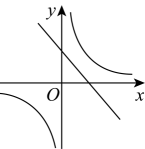 B、
B、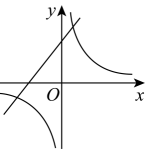 C、
C、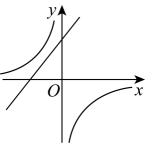 D、
D、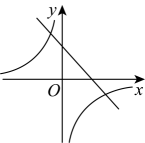 9. 如图,小明设计的用激光笔测量城墙高度的示意图,在点处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙的顶端处,已知 , , 米,米,米,那么该城墙的高度为( )
9. 如图,小明设计的用激光笔测量城墙高度的示意图,在点处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙的顶端处,已知 , , 米,米,米,那么该城墙的高度为( ) A、6 B、8 C、10 D、1810. 用配方法解方程时,配方后正确的是( )A、 B、 C、 D、11. 如图,的边上有两点、 , 且是正三角形,则下列条件不一定能使与相似的是( )
A、6 B、8 C、10 D、1810. 用配方法解方程时,配方后正确的是( )A、 B、 C、 D、11. 如图,的边上有两点、 , 且是正三角形,则下列条件不一定能使与相似的是( ) A、 B、 C、 D、12. 实数满足方程 , 则的值等于( )A、 B、 C、或 D、或
A、 B、 C、 D、12. 实数满足方程 , 则的值等于( )A、 B、 C、或 D、或二、填空题
-
13. 两个相似三角形对应高的比为 , 那么这两个三角形的周长比为 .14. 方程的解是 .15. 一个游泳池的容积为 , 游泳池注满水所用时间与注水速度(填“成正比例”、“成反比例”、“不成比例”).16. 若 ,则 .17. 某种植物的主干长出若干数目的支干,每个支干长出同样数量的小分支.若主干,支干和小分支的总数是73,设每个支干长出x个小分支,则可列方程为 .18. 如下图,跷跷板支架的高为0.3米,是的中点,那么跷跷板能骁起的最大高度等于米.
 19. 若关于的方程有两个相等的实数根,则的值为 .20. 如图,在正方形网格上,若使 , 则点P应在 .
19. 若关于的方程有两个相等的实数根,则的值为 .20. 如图,在正方形网格上,若使 , 则点P应在 .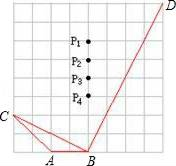
三、解答题
-
21. 解下列一元二次方程.(1)、(2)、22. 如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为 , 则坝高为多少 .
 23. 水果店店主张阿姨以每斤2元的价格购进某种水果若干,以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低元,每天可多售出20斤.为保证每天至少售出200斤,张阿姨决定降价销售.设这种水果每斤的售价降低元.(1)、每天的销售量为斤(用含的代数式表示);(2)、为尽量减少天气炎热带来的损耗,最大化减少库存,如果销售这种水果每天盈利300元,张阿姨需将每斤的售价降低多少元?24. 如图,一次函数与反比例函数图像交于点 , .
23. 水果店店主张阿姨以每斤2元的价格购进某种水果若干,以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低元,每天可多售出20斤.为保证每天至少售出200斤,张阿姨决定降价销售.设这种水果每斤的售价降低元.(1)、每天的销售量为斤(用含的代数式表示);(2)、为尽量减少天气炎热带来的损耗,最大化减少库存,如果销售这种水果每天盈利300元,张阿姨需将每斤的售价降低多少元?24. 如图,一次函数与反比例函数图像交于点 , . (1)、求的值;(2)、结合图像直接写出关于的不等式的解集.25. 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a , b , c分别为△ABC三边的长.(1)、如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
(1)、求的值;(2)、结合图像直接写出关于的不等式的解集.25. 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a , b , c分别为△ABC三边的长.(1)、如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.

