湖南省永州市宁远县2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2024-01-02 类型:期中考试
一、选择题(每题3分,共36分.将答案填在表格内)
-
1. 下列各式:① , ② , ③ , ④ , 其中分式有( )A、②④ B、③④ C、④ D、②2. 如果等腰三角形两边长是和 , 那么它的周长是( )A、 B、 C、或 D、3. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±14. 某新型纤维的直径约为0.000028米,将该新型纤维的半径用科学记数法表示是( )A、米 B、米 C、米 D、米5. 下列命题为真命题的是( )A、相等的角是对顶角 B、两条直线被第三条直线所截,内错角相等 C、和为的两个角互为邻补角 D、邻补角互补6. 若把的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、7. 如图,三个小朋友相约周末出去玩,图中点A、B、C代表三人的家所在的位置,为公平起见,集合地应定在以下什么位置,可以使三个小朋友的家到集合地的距离相等?( )
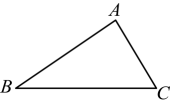 A、在三条高线所在的直线的交点处 B、在三条中线的交点处 C、在三条边的垂直平分线的交点处 D、在三条角平分线的交点处8. 下列各式,计算正确的是( )A、 B、 C、 D、9. 下面是假命题的是( )A、底边和一腰对应相等的两个等腰三角形全等 B、勾股定理和勾股定理的逆定理是一对互逆定理 C、经过旋转,对应线段平行且相等 D、一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等10. 下列关于x的方程是分式方程的是( )A、 B、 C、 D、11. 已知 , 若利用“”来判定 , 则需添加的条件是( )
A、在三条高线所在的直线的交点处 B、在三条中线的交点处 C、在三条边的垂直平分线的交点处 D、在三条角平分线的交点处8. 下列各式,计算正确的是( )A、 B、 C、 D、9. 下面是假命题的是( )A、底边和一腰对应相等的两个等腰三角形全等 B、勾股定理和勾股定理的逆定理是一对互逆定理 C、经过旋转,对应线段平行且相等 D、一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等10. 下列关于x的方程是分式方程的是( )A、 B、 C、 D、11. 已知 , 若利用“”来判定 , 则需添加的条件是( )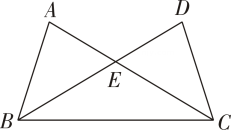 A、 B、 C、 D、12. 如果 , 那么代数式的值为( )A、 B、 C、 D、
A、 B、 C、 D、12. 如果 , 那么代数式的值为( )A、 B、 C、 D、二、填空题(每题3分,共24分.将答案填在横线上)
-
13. 计算: .14. 若一个三角形两边长分别为2、5,则此三角形的周长c的取值范围为 .15. 已知,在中, , , P为直线上一点,且 , 则的度数为 .16. 若关于x的方程有增根,则a的值为 .17. 如图在直角三角板中, , , . 如图,将三角板的顶点放置在直尺的一边上.当时,的度数为 .
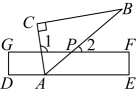 18. 如图, , 平分 , , 则 .
18. 如图, , 平分 , , 则 .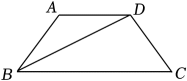 19. 分式方程的解为 .20. 如图,在3×3的网格中有A、B两点,任取一个格点E , 则满足△EAB是等腰三角形的点E有个.
19. 分式方程的解为 .20. 如图,在3×3的网格中有A、B两点,任取一个格点E , 则满足△EAB是等腰三角形的点E有个.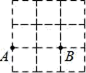
三、解答题
-
21. 计算下列各题.(1)、(2)、22. 先化简,再求值: , 其中 .23. 如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E .
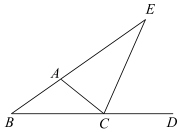 (1)、若∠B=35°,∠E=25°,求∠BAC的度数;(2)、证明:∠BAC=∠B+2∠E .24. 解方程:(1)、 .(2)、25. 某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型笔记本的单价比乙种类型的要便宜元,且用元购买的甲种类型的数量与用元购买的乙种类型的数量一样,求甲乙两种类型笔记本的单价.26. 已知,点为线段上的一点,以为边作等边 , 连接 , 以为边在的上方作等边 , 连接 , 交于点 .
(1)、若∠B=35°,∠E=25°,求∠BAC的度数;(2)、证明:∠BAC=∠B+2∠E .24. 解方程:(1)、 .(2)、25. 某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型笔记本的单价比乙种类型的要便宜元,且用元购买的甲种类型的数量与用元购买的乙种类型的数量一样,求甲乙两种类型笔记本的单价.26. 已知,点为线段上的一点,以为边作等边 , 连接 , 以为边在的上方作等边 , 连接 , 交于点 .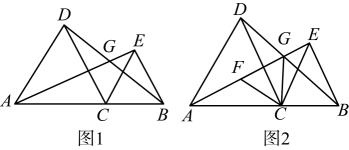 (1)、求证:;(2)、求的度数;(3)、如图2,连接 , 在线段上有一点 , 恰好使为等边三角形,若 , , 求的长.27. 请仔细阅读下面材料,然后解决问题:
(1)、求证:;(2)、求的度数;(3)、如图2,连接 , 在线段上有一点 , 恰好使为等边三角形,若 , , 求的长.27. 请仔细阅读下面材料,然后解决问题:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如: , ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: , . 我们知道,假分数可以化为带分数,例如:==2+=2 , 类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:==1+ .
(1)、将分式化为带分式;(2)、当x取哪些整数值时,分式的值也是整数?(3)、当x的值变化时,分式的最大值为 .