江西省九江市永修县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2024-01-02 类型:期中考试
一、单选题(本大题共6小题,每题3分,共18分)
-
1. 关于x的方程是一元二次方程,则a的取值范围是( )A、 B、 C、 D、2. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点 , , 都在横线上.若线段 , 则线段的长是( )
 A、3.5cm B、4cm C、4.5cm D、5cm3. 数学兴趣小组做“任意抛掷一枚图钉”的重复试验, 多次试验后获得如下数据:
A、3.5cm B、4cm C、4.5cm D、5cm3. 数学兴趣小组做“任意抛掷一枚图钉”的重复试验, 多次试验后获得如下数据:重复试验次数
10
50
100
500
1000
钉尖朝上次数
5
15
36
200
400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为( )
A、 B、 C、 D、4. 如图,在中,E在上,、交于F , 若 , , 且 , 则的长为( )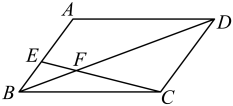 A、10 B、12 C、14 D、155. 春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,则可列方程( )A、 B、 C、 D、6. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )
A、10 B、12 C、14 D、155. 春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,则可列方程( )A、 B、 C、 D、6. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )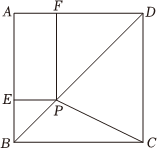 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每题3分,共18分)
-
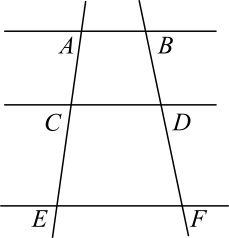
7. 如图,直线 , 若 , , 则的值是 .
 8. 箱子中装有除颜色外完全相同的三个小球,其中2个红球一个白球,从箱子中随机摸出两个球,这两个球的颜色相同的概率是.9. 如图,已知矩形矩形 , , , 则的长为 .
8. 箱子中装有除颜色外完全相同的三个小球,其中2个红球一个白球,从箱子中随机摸出两个球,这两个球的颜色相同的概率是.9. 如图,已知矩形矩形 , , , 则的长为 . 10. 设 , 分别为一元二次方程的两个实数根,则 .11. 如图,在平面直角坐标系中 A(3,0),B(0,4),AB=5,P 是线段 AB 上的一个动点,则 OP 的最小值是 .
10. 设 , 分别为一元二次方程的两个实数根,则 .11. 如图,在平面直角坐标系中 A(3,0),B(0,4),AB=5,P 是线段 AB 上的一个动点,则 OP 的最小值是 . 12. 如图,在坐标系中,正方形的边长为2,点是轴上一动点.若与的两边所组成的角的度数之比为 , 则点的坐标为 .
12. 如图,在坐标系中,正方形的边长为2,点是轴上一动点.若与的两边所组成的角的度数之比为 , 则点的坐标为 .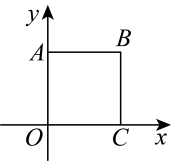
三、解答题(本大题共5小题,每题6分,共30分)
-
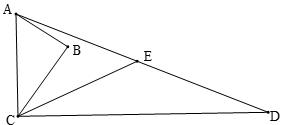
13.(1)、解方程: .(2)、若关于x的方程有两个相等的实数根,求m的值.14. 如图, 中, , , , , ,点E是AD的中点,求CE的长.
 15. 第31届世界大学生夏季运动会于2023年7月28日-8月8日在成都举行.彬彬和明明申请足球A、篮球B、排球C、乒乓球D . 四项赛事中某一项的志愿者,他们被随机分配到这四项赛事中的任意一项的可能性相同.(1)、“彬彬被分配到乒乓球D . 赛事做志愿者”是事件(填“必然”、“不可能”或“随机”).(2)、请用画树状图法或列表法,求彬彬和明明被分配到同一项赛事做志愿者的概率.16. 如图正方形 , 正方形如图,并排放置,G不是中点.请用无刻度直尺完成下列作图.
15. 第31届世界大学生夏季运动会于2023年7月28日-8月8日在成都举行.彬彬和明明申请足球A、篮球B、排球C、乒乓球D . 四项赛事中某一项的志愿者,他们被随机分配到这四项赛事中的任意一项的可能性相同.(1)、“彬彬被分配到乒乓球D . 赛事做志愿者”是事件(填“必然”、“不可能”或“随机”).(2)、请用画树状图法或列表法,求彬彬和明明被分配到同一项赛事做志愿者的概率.16. 如图正方形 , 正方形如图,并排放置,G不是中点.请用无刻度直尺完成下列作图.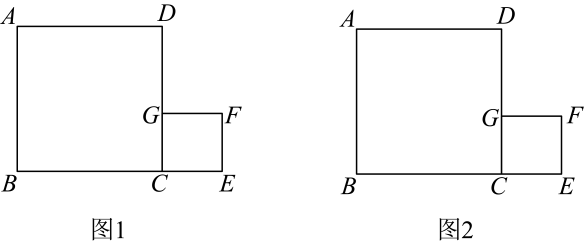 (1)、在图1中作平行四边形;(2)、在图2中边上寻找点P , 使得 .17. 如图所示,E是正方形ABCD的边AB上的一点,EF⊥DE交BC于点F.
(1)、在图1中作平行四边形;(2)、在图2中边上寻找点P , 使得 .17. 如图所示,E是正方形ABCD的边AB上的一点,EF⊥DE交BC于点F.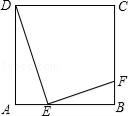 (1)、求证:△ADE∽△BEF;(2)、若AE:EB=1:2,求DE:EF的比值.
(1)、求证:△ADE∽△BEF;(2)、若AE:EB=1:2,求DE:EF的比值.四、解答题(本大题共3小题,每题8分,共24分)
-
18. 已知关于x的一元二次方程 .(1)、证明:不论a取任何实数,该方程都有两个不相等的实数根;(2)、若 , 为方程的两个根,且满足 , 求a的值.19. 如图,矩形中,点P , Q分别为边上的点, . BD平分 .
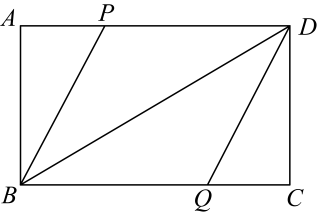 (1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积.20. 利客来超市销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,经过一段时间销售,发现销售单价每降低2元,平均每天可多售出4件.(1)、若降价6元,则平均每天销售数量的件;(2)、为了让顾客更实惠,每件商品降价多少元时,该商店每天销售利润为1200元?
(1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积.20. 利客来超市销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,经过一段时间销售,发现销售单价每降低2元,平均每天可多售出4件.(1)、若降价6元,则平均每天销售数量的件;(2)、为了让顾客更实惠,每件商品降价多少元时,该商店每天销售利润为1200元?五、解答题(本大题共2小题,每题9分,共18分)
-
21. 综合与实践
问题情景:小琴在延时服务剪纸课上发现了奇妙的数学知识,可以利用方程解决剪纸问题中的剩余面积问题.
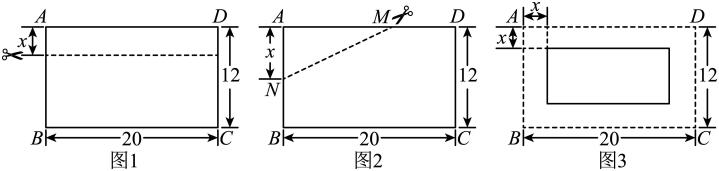 (1)、独立思考:如图1,长方形纸片长为 , 宽为 , 按如图方式剪下一个宽为的小长方形,若剩余长方形面积为 , 则x的值为 .(2)、实践探究:如图2,M为上一点,N为上一点,且 , 沿着剪下一个 , 若剩余部分图形面积为 , 求x的值.(3)、问题解决:如图3,将长方形纸片剪掉一个宽为的边框,剩余面积能否为 , 若能,请求出x的值;若不能,请说明理由.22. 如图1,2中四边形 , 点E , F , G , H分别为各边中点,顺次连接得到四边形EFGH .
(1)、独立思考:如图1,长方形纸片长为 , 宽为 , 按如图方式剪下一个宽为的小长方形,若剩余长方形面积为 , 则x的值为 .(2)、实践探究:如图2,M为上一点,N为上一点,且 , 沿着剪下一个 , 若剩余部分图形面积为 , 求x的值.(3)、问题解决:如图3,将长方形纸片剪掉一个宽为的边框,剩余面积能否为 , 若能,请求出x的值;若不能,请说明理由.22. 如图1,2中四边形 , 点E , F , G , H分别为各边中点,顺次连接得到四边形EFGH .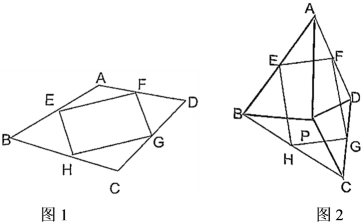 (1)、在图1中,判断四边形的形状,并说明理由;(2)、在图2中,P为四边形内一点,且满足 , . 判断四边形的形状,并说明理由.
(1)、在图1中,判断四边形的形状,并说明理由;(2)、在图2中,P为四边形内一点,且满足 , . 判断四边形的形状,并说明理由.六、综合题
-
23. 课本再现:如图正方形对角线与相交于点O , E为上任意点(不与B , C重合),作交于点F .
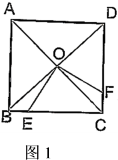
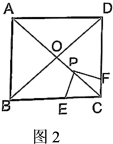
 (1)、在图1中解答下列问题:
(1)、在图1中解答下列问题:①)求证:
②)当正方形的面积为4时,小明发现以下结论:
①;②;③ . 其中正确的是 (填序号)
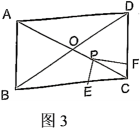
(2)、如图2,当点P为线段上任意点时(P不与O , C重合),E , F为分别为边上两点,且 . 问:之间有何数量关系,并说明理由.(3)、如图3,将图2中正方形改成矩形 , 且 , 其它条件不变,直接写出之间的数量关系.