重庆市南川区三校联盟2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-02 类型:期中考试
一、选择题:(本大题10个小题,每小题4分,共40分.在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段能组成三角形的是( )A、 B、 C、 D、3. 六边形的内角和为( )A、 B、 C、 D、4. 一个缺角的残片如图所示,量得 , 则这个三角形残缺前的的度数为( )
2. 下列长度的三条线段能组成三角形的是( )A、 B、 C、 D、3. 六边形的内角和为( )A、 B、 C、 D、4. 一个缺角的残片如图所示,量得 , 则这个三角形残缺前的的度数为( ) A、 B、 C、 D、5. 下列说法正确的是( )A、全等三角形的周长和面积相等 B、全等三角形是指面积相等的两个三角形 C、全等三角形是指形状相同的三角形 D、所有等边三角形是全等三角形6. 如图,点共线, , 添加一个条件,不能判定的是( )
A、 B、 C、 D、5. 下列说法正确的是( )A、全等三角形的周长和面积相等 B、全等三角形是指面积相等的两个三角形 C、全等三角形是指形状相同的三角形 D、所有等边三角形是全等三角形6. 如图,点共线, , 添加一个条件,不能判定的是( ) A、 B、 C、 D、7. 如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )
A、 B、 C、 D、7. 如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )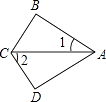 A、30° B、40° C、50° D、60°8. 十二边形的每个内角都相等,它的一个外角的度数是( )A、30° B、35° C、40° D、45°9. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )
A、30° B、40° C、50° D、60°8. 十二边形的每个内角都相等,它的一个外角的度数是( )A、30° B、35° C、40° D、45°9. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC=24,则△BMN的周长是( )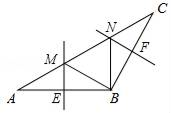 A、36 B、24 C、18 D、1610. 如图,在和中,三点在同一条直线上,连接 . 以下四个结论中:①;②;③;④ , 正确的个数是( ).
A、36 B、24 C、18 D、1610. 如图,在和中,三点在同一条直线上,连接 . 以下四个结论中:①;②;③;④ , 正确的个数是( ). A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题:(本大题8个小题,每小题4分,共32分.请将每小题的答案直接填在答题卡中对应的横线上)
-
11. 自行车的支架部分采用了三角形结构,是因为三角形具有性.
 12. 点的坐标是 , 它关于轴的对称点坐标是 .13. 若等腰三角形的两边长分别为3和5,则等腰三角形的周长为 .14. 如图,在 中, ,点 在线段 的延长线上, ,则 .
12. 点的坐标是 , 它关于轴的对称点坐标是 .13. 若等腰三角形的两边长分别为3和5,则等腰三角形的周长为 .14. 如图,在 中, ,点 在线段 的延长线上, ,则 .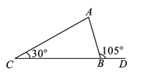 15. 如图在中,是边上的中线,且 , 点是中线上的两点,则图中阴影部分的面积是 .
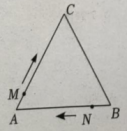
15. 如图在中,是边上的中线,且 , 点是中线上的两点,则图中阴影部分的面积是 .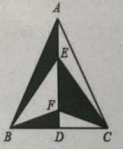 16. 如图,小亮从点出发,沿直线前进米后向左转 , 再沿直线前进米,又向左转 , , 照这样走下去,他第一次回到出发地点时,一共走了米.
16. 如图,小亮从点出发,沿直线前进米后向左转 , 再沿直线前进米,又向左转 , , 照这样走下去,他第一次回到出发地点时,一共走了米. 17. 如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC=.
17. 如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC=.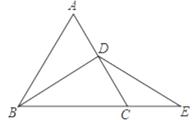 18. 如图,分别是边上的点, , 设的面积为 , 的面积为 , 若 , 则的值为 .
18. 如图,分别是边上的点, , 设的面积为 , 的面积为 , 若 , 则的值为 .
三、解答题:(本大题8个小题,第19题8分,20-26题各10分,共78分)解答出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
-
19. 在中, , 求各个内角的度数.20. 如图,在直角坐标系中,各顶点的横、纵坐标都是整数,
 (1)、作出关于轴对称的图形;(2)、求的面积21. 如图,已知点在线段上, . 求证: .
(1)、作出关于轴对称的图形;(2)、求的面积21. 如图,已知点在线段上, . 求证: . 22. 如图,已知分别为上的点,相交于点 .
22. 如图,已知分别为上的点,相交于点 .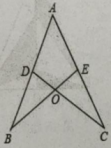 (1)、证明:;(2)、求证: .23. 如图,是的角平分线, , 垂足分别是 , 连接与相交于点 .
(1)、证明:;(2)、求证: .23. 如图,是的角平分线, , 垂足分别是 , 连接与相交于点 .
求证:
(1)、是等腰三角形(2)、