重庆市江津区五校联考2023-2024学年八年级上学期期中数学试题

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每题4分，共40分）

1. 如图， $△ A B C$ 中， $A D ⊥ B C$ 于点D ， $C E ⊥ A B$ 于点E ，则 $A B$ 边上的高是（）

A、 $A D$ B、 $C E$ C、 $D C$ D、 $A E$

查看试题解析
2. 下列各式中，计算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 $a^{5} - a^{4} = a$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a^{2} \cdot a^{4} = a^{6}$

查看试题解析
3. 下列长度的三条线段首尾顺次相接能组成三角形是（）

A、1，2，3 B、2，4，7 C、3，4，8 D、2，3，4

查看试题解析
4. 若一个n边形从一个顶点最多能引出5条对角线，则n是（）

A、5 B、8 C、9 D、10

查看试题解析
5. 尺规作图是起源于古希腊的数学课题，尺规作图中往往蕴含着丰富的数学知识和思想方法．如图，为了得到 $∠ P^{'} O^{'} Q^{'} = ∠ P O Q$ ，在用直尺和圆规作图的过程中，得到 $△ A O B ≌ △ A^{'} O^{'} B^{'}$ 的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
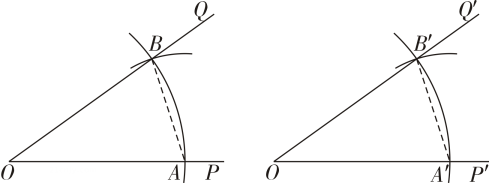6. 已知 $x - y = 7$ ， $x y = 5$ ，则 $(x + 1) (1 - y)$ 的值为（）

A、13 B、3 C、 $- 11$ D、 $- 13$

查看试题解析
7. 下列从左到右的变形中是因式分解的是（　　）

A、 $x^{2} + 1 = x (x + \frac{1}{x})$ B、 ${(x - y)}^{2} = x^{2} - 2 x y + y^{2}$ C、 $x^{2} - 9 y^{2} = (x + 3 y) (x - 3 y)$ D、 $x^{2} - y^{2} - 1 = (x + y) (x - y) - 1$

查看试题解析
8. 如图，在△ABC中，AC=5，中线AD=7，则AB边的取值范围是（）

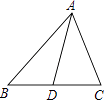A、1＜AB＜29 B、4＜AB＜24 C、5＜AB＜19 D、9＜AB＜19

查看试题解析
9. 如图，在四边形 $A B C D$ 中， $B D$ 平分 $∠ A B C$ ，且 $A D = C D$ ，若 $∠ C B D = α$ ，则 $∠ A D C$ 一定等于（）

A、 $3 α$ B、 $90 ° + 2 α$ C、 $135 ° - 2 α$ D、 $180 ° - 2 α$

查看试题解析
10. 如图，在Rt△ABC中，AB=CB ， BO⊥AC ，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F ，连接DE ， EF ．下列结论：①AB=2BD；②图中有4对全等三角形；③BD=BF； ④若将△DEF沿EF折叠，则点D不一定落在AC上；⑤S_四边形DFOE=S_△AOF ，上述结论中正确的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共8个小题，每题4分，共32分）

11. 计算： ${(π - 3)}^{0} + {(\frac{1}{2})}^{2} =$ ．

查看试题解析
12. 若一个正多边形的每一个外角都是 $36 °$ ，则该正多边形的边数是．

查看试题解析
13. 因式分解： $2 x^{2} - 18$ =

查看试题解析
14. 如图，已知 $A M$ 是 $Δ A B C$ 的中线，点 $P$ 是 $A C$ 边上一动点，若 $Δ A B C$ 的面积为10， $A C = 4$ ，则 $M P$ 的最小值为

查看试题解析
15. 若 $x^{2} - m x + 25$ 是完全平方式，则 $m =$ ．

查看试题解析
16. 已知实数 $a$ 、 $b$ 满足， $| a + b - 3 | + {(a b - 2)}^{2} = 0$ ，则 $a^{2} + b^{2}$ 值为．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A = 60 °$ ， $∠ A B C$ 和 $∠ A C B$ 的平分线 $B D$ 、 $C E$ 相交于点O ， $B D$ 交 $A C$ 于点D ， $C E$ 交 $A B$ 于点E ，若已知 $△ A B C$ 周长为20， $B C = 7$ ， $A E ： A D = 4 ： 3$ ，则 $A E$ 长为．

查看试题解析
18. 如果一个四位自然数 $\bar{a b c d}$ 的各数位上的数字均不为0，且满足 $\bar{a b} + \bar{b c} = \bar{c d}$ ，那么称这个四位数为“共和数”，例如：四位数1235， $∵ 12 + 23 = 35$ ， $∴ 1235$ 是“共和数”又如：四位数 $3824$ ， $38 + 82 \neq 24$ ， $∴ 3824$ 不是“共和数”，若一个“共和数”为 $m 268$ ，则 $m$ 的值为；若一个“共和数” $M$ 的前三个数字组成的三位数 $\bar{a b c}$ 与后三个数字组成的三位数 $b \bar{c d}$ 的差，再减去 $2 a$ ，结果能被7整除，则满足条件的 $M$ 的最大值与取小值的差是．

查看试题解析

三、解答题（本大题共8个小题，第19题8分，第20—26题各10分，共78分）

19. 计算

(1)、 $x y^{2} \cdot {(- 2 x y)}^{3}$

(2)、 $a (a - 2 b) + {(a + b)}^{2}$

查看试题解析
20. 尺规作图并完成证明．如图，点 $D$ 、点 $F$ 在 $△ A B C$ 外，连接 $A F$ 、 $A D$ 、 $B D$ ，且 $A F ∥ B C$ ， $∠ A B D = ∠ C A F$ ， $B D = A C$ ．

(1)、用尺规完成以下基本作图：
作 $∠ A B C$ 的平分线 $B E$ 交 $A F$ 于点 $E$ ，连接 $C E$ （保留作图痕迹，不写作法）；

(2)、根据（1）中作图，求证： $A D = C E$ ；请完善下面的证明过程．
证明： $∵$ $B E$ 平分 $∠ A B C$ ，
$∴$ $∠ C B E =$         ▲      ，
$∵$ $A F ∥ B C$ ，
$∴$ $∠ C B E =$         ▲
$∴$ $∠ A B E = ∠ A E B$ ，
$∴$ $A E = A B$ ，
在 $△ A C E$ 和 $△ B D A$ 中，
${\begin{array}{l} A E = A B \\ ∠ A B D = ∠ C A F \\ ___________ \end{array}$ ，
$∴$ $△ A C E ≌ △ B D A$ ．
$∴$ $A D = C E$ （        ▲     ）

查看试题解析
21. 先化简，再求值： $[(3 a - 2 b) (3 a + 2 b) + {(2 a - b)}^{2} - b (2 a - 3 b)] \div (- \frac{1}{2} a)$ ，其中a、b满足 ${(a + 1)}^{2} + b^{2} + 9 = 6 b$

查看试题解析
22. 如图，在△ABC中，∠B＝40°，∠C＝70°，AD为∠BAC的平分线，AE为BC边上的高，求∠DAE的度数．

查看试题解析
23. 已知 $a - b = 7$ ， $a b = 6$ ．

(1)、求 $a^{2} + b^{2}$ 的值；

(2)、求 $a^{4} b^{2} - a^{3} b^{3} + a^{2} b^{4}$ 的值．

查看试题解析
24. 如图，点 $E$ 在 $△ A B C$ 边 $A C$ 上， $A E = B C$ ， $B C ∥ A D$ ， $∠ C E D = ∠ B A D$ ．

(1)、求证： $△ A B C ≌ △ D E A$ ；

(2)、∠ $A C B = 30 °$ ， $∠ A D E = 20 °$ ，求 $∠ B A D$ 的度数．

查看试题解析
25. 从边长为a的正方形中剪掉一个边长为b的正方形(如图①)，然后将剩余部分拼成一个长方形(如图②).

(1)、上述操作能验证的等式是 ▲ ；

(2)、应用你从(1)得出的等式，完成下列各题：
①已知x²−4y²=12，x+2y=4，求x−2y的值.
②计算：(1− $\frac{1}{2^{2}}$ )(1− $\frac{1}{3^{2}}$ )(1− $\frac{1}{4^{2}}$ )…(1− $\frac{1}{1 9^{2}}$ )(1− $\frac{1}{2 0^{2}}$ )．

查看试题解析
26. $△ A B C$ 和 $△ D B E$ 都是以点B为顶点的等腰直角三角形， $∠ A B C = ∠ D B E = 90 °$ ．

(1)、如图1，当边 $B D$ 恰好在 $△ A B C$ 的 $B C$ 边上时，连接 $A D$ ， $A C$ ，易证 $△ A B D ≌ △ B C E$ ，从而证明 $C E ⊥ A D$ ；（无需证明）

(2)、如图2，当 $△ A B C$ 和 $△ D B E$ 如图摆放，连接 $C D$ 、 $A D$ 、 $C E$ ，其中 $A D$ 与 $C E$ 相交于点F ．那么 $A D$ 与 $C E$ 的位置关系是否发生变化，请说明理由；

(3)、如图3，当 $△ A B C$ 和 $△ D B E$ 如图摆放，F为 $A C$ 的中点，连接 $A D$ 、 $C E$ 、 $F D$ ，并在 $F D$ 的延长线上取一点G ，连结 $C G$ ，使 $C G = C E$ ，求证： $∠ F D A = ∠ C G F$ ．

查看试题解析