重庆市九龙坡区重点中学2023-2024学年八年级上学期期中数学试题

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（本大题10个小题，每小题4分，共40分，在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑）．

1. 下面四大通讯运营商的企业图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段中，能组成三角形的是（）

A、15，8，20 B、3，4，7 C、7，4，2 D、1，5，7

查看试题解析
3. 下列运算正确的是（）

A、 $a^{7} \div a = a^{7}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 ${(a b)}^{2} = a b^{2}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
4. 在平面直角坐标系中，点 $P (2 ， - 3)$ 关于y轴对称的点的坐标是（）

A、 $(2 ， 3)$ B、 $(2 ， - 3)$ C、 $(- 2 ， 3)$ D、 $(- 2 ， - 3)$

查看试题解析
5. 若 $(x - 4) (x + 3) = x^{2} + m x - 12$ ，则m的值是（）

A、1 B、－1 C、9 D、－9

查看试题解析
6. 下列说法中，正确的是（）

A、三角形的三条高都在三角形内 B、三角形的一个外角大于任何一个内角 C、三角形的一条中线把三角形分成面积相等的两个三角形 D、到三角形三边距离相等的点是这个三角形三条边的垂直平分线的交点

查看试题解析
7. 如图，在△ABC和△DEF中，如果AB＝DE ， BC＝EF ．在下列条件中不能保证△ABC≌△DEF的是（）

A、∠B＝∠DEF B、 $A B ∥ D E$ C、∠A＝∠D D、AC＝DF

查看试题解析
8. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，……按此规律排列，则第⑦个图形中小圆圈的个数为（）

A、24 B、26 C、27 D、30

查看试题解析
9. 如图，在△ABC中，AB边的中垂线DE，分别与AB、AC边交于点D、E两点，BC边的中垂线FG，分别与BC、AC边交于点F、G两点，连接BE、BG．若△BEG的周长为16，GE＝1．则AC的长为（）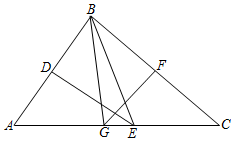

A、13 B、14 C、15 D、16

查看试题解析
10. 如图，Rt△ABC中，∠BAC＝90°，AD⊥BC于点D ，过点A作 $A F ∥ B C$ 且AF＝AD ，点E是AC上一
点且AE＝AB ，连接EF ， DE ．连接FD交BE于点G ．下列结论中正确的有（）个．
①BD＝EF：②∠AEB＝∠AEF：③FD平分∠AFE；④ $S_{四边形 A B D E} = S_{四边形 A D E F}$ ：⑤BG＝GE ．

A、2 B、3 C、4 D、5

查看试题解析

二、填空题（本大题8个小题，每小题4分，共32分，将每小题的答案直接填在答题卡中对应的横线上）

11. $- 3 a b \cdot 2 a^{2} b =$ ．

查看试题解析
12. 一个多边形的内角和是1080°，则这个多边形的边数为．

查看试题解析
13. 已知 $a^{m} = 2$ ， $a^{n} = 5$ ，则 $a^{3 m + 2 m} =$ ．

查看试题解析
14. 如图，在△ABC中，∠C＝90°，AD平分∠CAB交BC于点D ， DE⊥AB ，垂足为E ，若BC＝4，DE＝1.6，则BD的长为．

查看试题解析
15. 如图，将一副三角尺如图所示叠放在一起，若AB＝12cm，则阴影部分的面积是cm² ．

查看试题解析
16. 如图，在△ABC中，AB＝4，AC＝6，BC＝7，EF垂直平分BC ，点D为直线EF上的任意一点，则△ABD周长的最小值是．

查看试题解析
17. 已知关于x ， y的方程组 ${\begin{array}{l} 2 x + 3 y = 5 \\ 3 x + 2 y = a \end{array}$ 的解满足 $y - x > 0$ ，且关于x的不等式组 ${\begin{array}{l} \frac{x + 3}{2} - 2 > a \\ x + 1 < a \end{array}$ 无解，那么所有符合条件的整数a的和为．

查看试题解析
18. 如果一个三位数的十位数字等于它的百位和个位数字的差的绝对值，那么称这个三位数为“三决数”，如：三位数312， $∵ 1 = | 3 - 2 |$ ， $∴$ 312是“三决数”，把一个三决数m的任意一个数位上的数字去掉，得到三个两位数，这三个两位数之和记为 $F (m)$ ，把m的百位数字与个位数字之差的2倍记为 $G (m)$ ．则 $F (145) + G (145)$ 的值为；若三位数A是“三决数”，且 $F (A) + G (A)$ 是一个正整数的平方，且百位数字小于个位数字，请求出所有符合条件的A的最大值与最小值的差为．

查看试题解析

三、解答题（本大题共8个小题，19小题8分，其余每小题10分，共78分）

19. 计算：

(1)、 $(- 2 x y^{2})^{3} \cdot 5 x^{2} y$

(2)、 $(- 6 x^{4} + 8 x^{3}) \div (- 2 x^{2}) + (3 x + 2) (1 - x)$

查看试题解析
20. 已知：如图，AB＝AD ， AC＝AE ， ∠1＝∠2．求证：BC＝DE

查看试题解析
21. 如图，在△ABC中，∠ABC＝90°．

(1)、尺规作图：作AC的垂直平分线交AC于点E ，交BC于点D ，连接AD ．（保留作图痕迹，不写作法，不用下结论）；

(2)、在（1）的条件下，若AD平分∠CAB ．求证：AC＝2AB
证明： $∵$ DE为AC的垂直平分线
$∴$ DE⊥AC
$∵$ ∠ABC＝90°， $∴$ AB⊥BC ，
$∵$ AD平分∠CAB
$∴$ ① ▲
在Rt△ABD与Rt△AED中 ${\begin{array}{l} D E = D B \\ A D = A D \end{array}$
$∴$ Rt△ABD≌Rt△AED（② ▲ ）
$∴$ ③ ▲
$∵$ DE为AC的垂直平分线
$∴$ AE＝④ ▲
$∴$ AC＝2AB

查看试题解析
22. 如图，在平面直角坐标系xOy中，每个小正方形的边长均为1个单位长度，已知△ABC三个顶点的坐标分别为 $A (- 3 ， 4)$ ， $B (- 5 ， 2)$ ， $C (- 2 ， 1)$ ．
⑴将△ABC向右平移5个单位再向下平移1个单位得到 $△ A_{1} B_{1} C_{1}$ ，在图中作出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $C_{1}$ 的坐标 ▲ ；
⑵在图中作出△ABC关于x轴的对称图形 $△ A_{2} B_{2} C_{2}$ ，点A、B、C的对应点分别为 $A_{2} 、 B_{2} 、 C_{2}$ ；
⑶求 $△ A_{2} B_{2} C_{2}$ 的面积．

查看试题解析
23.

(1)、【模型启迪】如图1，在△ABC中，D为BC边的中点，连接AD并延长至点H ，使DH＝AD ，连接BH ，则AC与BH的数量关系为，位置关系为．

(2)、【模型探索】如图2，在△ABC中，D为BC边的中点，连接AD ， E为AC边上一点，连接BE交AD于点F ，且BF＝AC ．求证：AE＝EF ．

查看试题解析
24. 如图，△ABC与△AED中，∠E＝∠C ， DE＝BC ， EA＝CA ，过A作AF⊥DE垂足为F ， DE交CB的延长线于点G ，连接AG ．

(1)、求证：△ABC≌△ADE；

(2)、求证：GA平分∠DGB；

(3)、若四边形DGBA的面积为18，AF＝4.5，求FG的长．

查看试题解析
25. 对于一个图形，通过不同的方法计算图形的面积可以得到一个数学等式．
例如，由图1可以得到： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$

(1)、由图2可以得到：

(2)、利用图2所得的等式解答下列问题：
①若实数a ， b ， c满足 $a + b + c = 11$ ， $a b + b c + a c = 38$ ，求 $a^{2} + b^{2} + c^{2}$ 的值；
②若实数x ， y ， z满足 $2^{x} \times 4^{y} \div 8^{z} = 4$ ， $x^{2} + 4 y^{2} + 9 z^{2} = 44$ ，求 $2 x y - 3 x z - 6 y z$ 的值．

查看试题解析
26. 如图1，已知等边△ABC ，以B为直角顶点向右作等腰直角△BCD ，连接AD ．

(1)、若 $A C = 8 \sqrt{3}$ ，求点D到AB边的距离；

(2)、如图2，过点B作AD的垂线，分别交AD ， CD于点E ， F ，探索EF ， CF ， BE之间的数量关系并证明；

(3)、如图3，点M ， N分别为线段AD ， BD上一点，AM＝BN ，连接CM ， CN ，若 $A C = 6 \sqrt{2}$ ，当CM＋CN取得最小值时，直接写出△ACM的面积．（提示：直角三角形中两直角边的平方和等于斜边的平方）

查看试题解析