重庆市开州区德阳教育集团2023-2024学年七年级上学期期中数学试题

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题：每小题4分，共40分，在每个小题的下面都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答案填涂在答题卡上对应的方框中

1. -3的相反数是（）

A、3 B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、-3

查看试题解析
2. 用四舍五入法，把3.1459精确到百分位，取得的近似数是（）

A、3.1 B、3.146 C、3.14 D、3.15

查看试题解析
3. 下列哪个是单项式（）

A、 $x + 2$ B、 $a^{2}$ C、 $- \frac{1}{x}$ D、 $y = 2 - x$

查看试题解析
4. 下列计算正确的是（）

A、 $2 a b + 3 a b = 5 a b$ B、 $7 y^{2} - 2 y^{2} = 5$ C、 $4 a + 2 a = 6 a^{2}$ D、 $3 m^{2} n - 2 m n^{2} = m n^{2}$

查看试题解析
5. 在数5， $π$ ， 0，-3.14， $\frac{7}{23}$ ， 0.3，-20中，其中整数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 化简： $- (a - b - c)$ 的结果是（）

A、 $a - b - c$ B、 $- a - b - c$ C、 $a + b + c$ D、 $- a + b + c$

查看试题解析
7. 某商品标价为m元，商店以标价7折的价格开展促销活动，这时一件商品的售价为（　　）

A、0.3m元 B、1.7m元 C、7m元 D、0.7m元

查看试题解析
8. 下列几个算式中，正确的有（）个．
① $- 3 - 7 = - 10$ ；② $5 + (- 7) = - 2$ ；③ $- 3 \times 3 = 9$ ；④ $- 3 \div (- 3) = - 1$

A、0 B、1 C、2 D、3

查看试题解析
9. 下列图形都是由同样大小的正方形按一定的规律排列组成，其中第①个图形中有3个正方形，第②个图形中有7个正方形，第③个图形中有11个正方形，⋯，按此规律，第⑧个图形中共有（）个正方形．

A、30 B、31 C、32 D、33

查看试题解析
10. 有理数a ， b ， c在数轴上对应的点的位置如图所示，则下列各式正确的有（）
① $a b c > 0$ ；② $a + b < c$ ；③ $\frac{| a |}{a} + \frac{| b |}{b} - \frac{| c |}{c} = - 1$ ；④ $b < - a < - c < c < a < - b$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每小题4分，共32分，请将每小题的答案直接填在答题卡中对应的横线上）

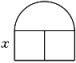
11. 据统计2023年底全国共有学生团员48620000名，48620000用科学记数法表示为．

查看试题解析
12. 若向东走4米记作“+4米”，向西走5米记作“-5米”，则向西走13米可记作米．

查看试题解析
13. $- \frac{5 x y}{3}$ 的系数是．

查看试题解析
14. 比较大小 $- \frac{1}{8}$ $- \frac{1}{9}$ （填写“>”，“<”或“=”号）．

查看试题解析
15. 多项式 $x^{4} y^{2} - x^{2} y + 2 y^{4}$ 的次数是．

查看试题解析
16. 窗户的形状如图所示，其上部是半圆形，下部是边长相同的两个小正方形，已知下部小正方形的边长是x ．窗户的面积为（结果保留π）．

查看试题解析
17. 若 ${(x - 3)}^{2} + | y + 2 | = 0$ ，则 $y^{x}$ 的值为．

查看试题解析
18. 点P在数轴上从0开始，第1次向右移动1个单位，紧接着第2次向左移动2个单位，第3次向右移动3个单位，第4次向左移动4个单位，⋯，依此规律移动，当它移动160次时，落在数轴上的点表示的数是．

查看试题解析

三、解答题：（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上．

19. 计算：

(1)、 $6 + (- 9) + (- 4) - 7$ ；

(2)、 $4 \frac{3}{5} + (- 7 \frac{2}{7}) + 5 \frac{2}{5} - (+ 3 \frac{5}{7})$

查看试题解析

四、解答题：（本大题共个7小题，每小题10分，共70分）解答时必须给出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上．

20. 计算：

(1)、 $3 + (- 6) \times 2 - (- 24) \div 6$

(2)、 $- 1^{6} \times (- 7) + [2^{2} - (- 8)] \div (- 3)$

查看试题解析
21. 化简或求值

(1)、化简： $x^{2} - 4 x + (3 x^{2} - 5 x + 5)$

(2)、先化简，再求值： $3 (2 x y^{2} + 2 y^{3}) - (2 y^{3} + x y^{2}) - 4 y^{3}$ ，其中 $x = 4$ ， $y = - 3$ ．

查看试题解析
22. 已知m ， n互为相反数，p ， q互为倒数，x的绝对值等于2，求 $- 2 p q + \frac{m + n}{p q} - x$ 的值．

查看试题解析
23. 某检修站，工人乘一辆汽车沿东西方向的公路检修线路，约定向东为正，向西为负，从A地出发到收工时，行走记录为（单位：千米）：
+16，-3，+5，-2，+10，-3，-2，-12

(1)、计算收工时，工人在A地的哪一边，距A地多远？

(2)、若汽车每行驶100千米耗油6升，求这一天汽车共耗油多少升？

查看试题解析
24. 已知： $A = 5 x^{2} - m x + 2$ ， $B = x^{2} - 3 x - 3$ ．

(1)、若m=3时，求 $A - B$ ；

(2)、若 $A - 5 B$ 的值与x的值无关，求m的值．

查看试题解析
25. 对于任意有理数a、b、c、d ，我们规定符号 $(a ， b) \otimes (c ， d) = a d - b c + 5$ ，
例如： $(1 ， 3) \otimes (2 ， 4) = 1 \times 4 - 2 \times 3 + 5 = 3$ ．

(1)、求 $(- 2 ， 1) \otimes (3 ， 5)$ 的值；

(2)、求 $(3 a^{2} + 2 a ， 1) \otimes (2 a^{2} + 4 a ， 2)$ 的值，其中 $a = 3$ ．

查看试题解析
26. 数轴上表示数a的点与原点的距离叫做数a的绝对值，记作 $| a |$ ，数轴上表示数a的点与表示数b的点的距离记作 $| a - b |$ ，如数轴上表示数5的点与表示数7的点的距离为|5-7|=2，
$| 5 + 7 | = | 5 - (- 7) |$ 表示数轴上表示数5的点与表示数-7的点的距离，
$| a - 5 |$ 表示数轴上表示数a的点与表示数5的点的距离．
根据以上材料回答下列问题：

(1)、若 $| x - 2 | = 3$ ，则 $x =$ ， $| x - 4 | = | x + 2 |$ ，则 $x =$ ．

(2)、若 $| x - 3 | + | x + 2 | = 5$ ，则x能取到的最小值是，最大值是．

(3)、若 $| x - 3 | + | x + 2 | = 9$ ，则x的值为多少？

查看试题解析