山东省济南市历下区2023-2024学年八年级上学期期中数学试题

试卷更新日期：2024-01-02 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. 在平面直角坐标系中，点 $A (1 ， 2)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各式中，是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{2}$ D、 $\sqrt{8}$

查看试题解析
3. 下列关于 $x$ 的函数是一次函数的是（）

A、 $y = \frac{2}{x}$ B、 $y = \sqrt{x + 1}$ C、 $y = x^{2} - 1$ D、 $y = 5 x - 2$

查看试题解析
4. ${\begin{array}{l} x = 5 \\ y = 3 \end{array}$ 是下面哪个二元一次方程的解（）

A、 $2 x - y = 7$ B、 $y = - x + 2$ C、 $x = - y - 2$ D、 $2 x - 3 y = - 1$

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ C、 $\frac{1}{\sqrt{2}} = \sqrt{2}$ D、 $\sqrt{4} + \sqrt{2} = 2$

查看试题解析
6. 一次函数 $y = m x + m^{2} (m \neq 0)$ 的图象过点 $(0 ， 4)$ ，且 $y$ 随 $x$ 的增大而减小，则 $m$ 的值为（）

A、 $- 2$ B、 $- 2$ 或2 C、1 D、2

查看试题解析
7. 将第一象限的“小旗”各点的横坐标保持不变，纵坐标分别乘以 $- 1$ ，符合上述要求的图形是（）

A、 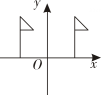B、 C、 D、

查看试题解析
8. 某校规定学生体测成绩由三部分组成：长跑占成绩的 $50 %$ ， 50米跑占成绩的 $25 %$ ，立定跳远占成绩的 $25 %$ ．小明上述三项成绩依次是92分，100分，80分，则小明本次的体测成绩为（）分．

A、95 B、93 C、91 D、89

查看试题解析
9. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = m x + n$ 的图象如图所示，下列选项正确的是（）
①对于函数 $y_{1} = k x + b$ 来说， $s$ 随 $t$ 的增大而减小；
②函数 $y = k x + n$ 的图象不经过第一象限；
③ $2 k - 2 m = n - b$

A、①② B、①③ C、②③ D、①②③

查看试题解析
10. $A B$ 两地相距240千米，早上9点，甲车从 $A$ 地出发去 $B$ 地，20分钟后，乙车从 $B$ 地出发去 $A$ 地．甲、乙两车离开各自出发地的路程 $s_{1} 、 s_{2}$ （千米）与甲车出发的时间 $t$ （小时）之间的关系如图所示，下列描述中不正确的有（）个．

①甲车的平均速度是60千米/小时；
②乙车的平均速度是80千米/小时；
③甲车与乙车在早上10点相遇；
④两车在10：40或10：58时相距20千米．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共6个小题，每小题4分，共24分．）

11. 如图，在“笑脸”的“嘴巴”上找一格点，这一格点的坐标可以为（写出一点即可）．

查看试题解析
12. 赵老师每天登录“学习强国”进行学习，在获得信息和知识的同时，还能获得“点点通”奖励．上表是王老师最近一周每日“点点通”奖励情况，这组数据的平均数是点．
星期
一
二
三
四
五
六
日
“点点通”（点）
15
20
25
23
21
17
19

查看试题解析
13. 列方程组解题：“今有马二、牛一，直金七两；马三、牛二，直金十二两．马、牛各直金几何？”其大意是：2匹马，1头牛，一共价值7两；3匹马，2头牛，一共价值12两，问每匹马、每头牛各价值多少两？设每匹马 $x$ 两，每头牛 $y$ 两．根据题意，可列方程组为．

查看试题解析
14. 直线 $y = x + 1$ 与直线 $y = m x + n$ 相交于点 $M (1 ， b)$ ，则关于 $x ， y$ 的方程组 ${\begin{array}{l} x + 1 = y \\ y - m x = n \end{array}$ 的解为．

查看试题解析
15. 下表列出了一项实验的统计数据（单位： $c m$ ）：
$x$
50
80
100
150
…
$y$
30
45
55
80
…
它表示皮球从一定高度落下时，弹跳高度 $y$ 是下落高度 $x$ 的一次函数，那么变量 $y$ 与 $x$ 之间的关系式为．

查看试题解析
16. 如图，在平面直角坐标系中，直线 $A B$ 表达式为 $y = \frac{1}{3} x$ ，点 $M (3 ， 1)$ 是直线 $A B$ 上一点，直线 $C D$ 过点 $M$ ，且与直线 $A B$ 的夹角 $∠ A M C = 45 °$ ，则直线 $C D$ 的表达式为．

查看试题解析

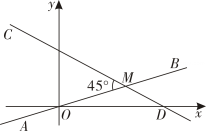
三、解答题（本大题共10个小题，共86分．请写出文字说明、证明过程或演算步骤．）

17. 计算：

(1)、 $(2 + \sqrt{3}) (2 - \sqrt{3})$

(2)、 $\sqrt{18} - \sqrt{50} + 4 \sqrt{\frac{1}{2}}$

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} x = y + 1 \\ x + 2 y = 7 \end{array}$

(2)、 ${\begin{array}{l} 3 x - 5 y = - 1 \\ 4 x + 5 y = 8 \end{array}$

查看试题解析
19. ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ 和 ${\begin{array}{l} x = 1 \\ y = 4 \end{array}$ 都是方程 $a x - y = b$ 的解，求 $a$ 与 $b$ 的值．

查看试题解析
20. 如图，直线 $l$ 是一次函数 $y = k x + b$ 的图象，且经过点 $A (0 ， 4)$ 和点 $B (- 5 ， - 2)$ ．

(1)、求 $k$ 和 $b$ 的值；

(2)、求直线 $l$ 与两坐标轴所围成的三角形的面积．

查看试题解析
21. 如图，在平面直角坐标系中， $A (- 4 ， 1) ， B (- 3 ， 3) ， C (- 2 ， - 2)$ ．
⑴作出 $△ A B C$ ；
⑵作出 $△ A B C$ 关于 $y$ 轴的对称图形 $△ A_{1} B_{1} C_{1}$ ；
⑶求 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
22. 2023年中秋、国庆双节假期期间，济南趵突泉景区共纳客200多万人次，为迎接游客，甲、乙两个纪念品商店对标价都是每个10元纪念印章推出优惠活动：甲商店购买5个以上，从第6个开始按标价的9折卖：乙商店从第1个开始就按标价的9.5折卖．

(1)、直接写出两商店优惠后的价格 $y$ （元）与购买数量 $x$ （个）的关系式（ $x > 5$ ）；

(2)、小明要买8个纪念印章，到哪个商店购买比较省钱，请说明理由；

(3)、若纪念印章的成本为每个7元，请写出甲商店的利润 $w$ （元）与卖出数量 $x$ （个）的关系（卖出5个以上）．

查看试题解析
23. 2023年10月1日是中华人民共和国成立74周年，学校开展了“迎国庆·弘扬中华传统文化”知识竞赛活动，学校从初中三个年级各随机抽取10人进行相关测试，获得了他们的成绩（单位：分），并对数据（成绩）进行整理、描述和分析，下面给出了相关信息：
a.30名同学中华传统文化知识测试成绩的统计图如图1：
b.30名同学中华传统文化知识测试成绩的频数分布直方图如图2（数据分成6组： $40 \leq x < 50$ ， $50 \leq x < 60 ， 60 \leq x < 70 ， 70 \leq x < 80 ， 80 \leq x < 90 ， 90 \leq x < 100$ ）．
c ．测试成绩在 $70 \leq x < 80$ 这一组的是：
70 72 72 74 74 74 75 77
d ．小明的中华传统文化知识测试成绩为77分．
根据以上信息，回答下列问题：

(1)、测试成绩在 $70 \leq x < 80$ 这一组的同学成绩的众数为分；

(2)、小明的测试成绩在抽取的30名同学的成绩中从高到低排名第名；

(3)、抽取的30名同学的成绩的中位数为分；

(4)、序号（见图1横轴）为1-10的学生是七年级的，他们成绩的方差记为 ${s_{1}}^{2}$ ；序号为11-20的学生是八年级的，他们成绩的方差记为 ${s_{2}}^{2}$ ；序号为21-30的学生是九年级的，他们成绩的方差记为 ${s_{3}}^{2}$ ．直接写出① ${s_{1}}^{2}$ ， ② ${s_{2}}^{2}$ ， ③ ${s_{3}}^{2}$ 中最小的是（填序号）；

(5)、成绩80分及以上记为优秀，若该校初中三个年级1800名同学都参加测试，请估计成绩优秀的同学人数．

查看试题解析

24. 根据以下素材，探索完成任务．

如何设计布料剪裁方案？
素材1	图1中是第31届世界大学生夏季运动会吉祥物“蓉宝”玩偶，经测量，制作该款吉祥物头部所需布料尺寸为 $50 c m \times 15 c m$ ，身子布料尺寸 $50 c m \times 40 c m$ ．图2是两部分布料的尺寸示意图．
素材2	某工厂制作该款式吉祥物，经清点库存时发现，需在市场上购进某型号布料加工制作该款式的玩偶．已知该布料长为 $240 c m$ ，宽为 $50 c m$ ．（剪裁时不计损耗）
我是布料剪裁师
任务一	拟定剪裁方案	若要不造成布料浪费，请你设计出一匹该布料的所有剪裁方案：方案一：剪裁头部布料16张和身子布料0张．方案二：剪裁头部布料 ▲ 张和身子布料 ▲ 张．方案三：剪裁头部布料 ▲ 张和身子布料 ▲ 张．
任务二	解决实际问题	工厂目前已有裁剪好的12张头部布料和4张身子布料，经商议，现需购买一批该型号布料，其中一部分按照方案二裁剪，另一部分按照方案三裁剪，一共制作700个“蓉宝”玩偶．请问：需要购买该型号布料共多少匹（恰好全部用完）？

查看试题解析

25. 为激发学生们对科技的好奇心和探索欲，培养学生的创新意识和创新精神，某学校开展了“智能小车实验探究”活动．某小组观察探究小车运动中的函数关系，如图，在一条长为 $50 c m$ 的水平直线轨道上，放置一辆长为 $4 c m$ 的智能小车，开始时小车左端与 $A$ 处挡板重合，然后以 $2 c m / s$ 的速度匀速向右行驶，当小车接触到 $B$ 处的挡板时因为要改变方向需停顿 $1 s$ ，然后以相同的速度返回，至再次与 $A$ 处的挡板接触时小车停止运动．在这个过程中，设小车的右端与 $B$ 处挡板的距离为 $s (c m)$ ，小车出发后的时间为 $t (s)$ ，请根据所给条件解决下列问题：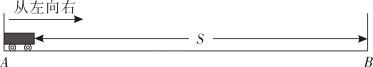

(1)、小车运动时间为 $3 s$ 时， $s$ 的值为 $c m$ ；

(2)、小车从 $B$ 处驶向 $A$ 处的过程中，求 $s$ 与 $t$ 的函数表达式；

(3)、当小车左端与 $A$ 处挡板的距离比小车右端与 $B$ 处挡板距离的2倍多 $4 c m$ 时，请求出 $t$ 的值．

查看试题解析
26. 如图，直线 $l_{1} ： y = - \sqrt{3} x + 4 \sqrt{3}$ 与 $x$ 轴、 $y$ 轴分别交于点 $A 、 B ， ∠ B A O = 60 °$ ，直线 $l_{2} ： y = k x - k + 3 \sqrt{3}$ 与 $x$ 轴、 $y$ 轴分别交于点 $C 、 D$ ．

(1)、直线 $y = k x - k + 3 \sqrt{3}$ 过定点 $M$ 的坐标为 ▲ （填写合适的选项）；

A、 $(1 ， 3)$ B、 $(1 ， 3 \sqrt{3})$ C、 $(\frac{3}{2} ， \frac{3 \sqrt{3}}{2})$ D、 $(2 ， 2 \sqrt{3})$

(2)、若直线 $l_{2}$ 将 $△ A O B$ 的面积分为 $1 ： 7$ 两部分，请求出 $k$ 的值．

(3)、当 $k > 0$ 时，将直线 $l_{2}$ 沿直线 $l_{1}$ 作轴对称得直线 $l_{3}$ ，此时直线 $l_{3}$ 与 $x$ 轴平行，直接写出此时 $l_{2} ： y = k x - k + 3 \sqrt{3}$ 的 $k$ 值．

查看试题解析

星期	一	二	三	四	五	六	日
“点点通”（点）	15	20	25	23	21	17	19

$x$	50	80	100	150	…
$y$	30	45	55	80	…