安徽省合肥市五十中教育集团望岳校区2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-02 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 在平面直角坐标系中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 将点先向左平移2个单位长度,再向下平移3个单位长度后得到的点的坐标为( )A、 B、 C、 D、3. 一副三角板,按如图所示叠放在一起,则图中∠α的度数为( )
 A、10° B、15° C、20° D、25°4. 函数的自变量的取值范围是( )A、 B、 C、 D、5. 已知等腰的两边长分别为4和9,则等腰的周长为( )A、17或22 B、17 C、22 D、无法确定6. 下列选项中,可以用来说明命题“若 , 则”是假命题的反例是( )A、 B、 C、 D、7. 若 , 分别是一次函数图象上两个不相同的点,记 , 则为( )A、正数 B、负数 C、0 D、非负数8. 给定下列条件,不能判定三角形是直角三角形的是( )A、 B、 C、 D、9. 如图,一次函数与的图象相交于 , 则函数的图象可能是( )
A、10° B、15° C、20° D、25°4. 函数的自变量的取值范围是( )A、 B、 C、 D、5. 已知等腰的两边长分别为4和9,则等腰的周长为( )A、17或22 B、17 C、22 D、无法确定6. 下列选项中,可以用来说明命题“若 , 则”是假命题的反例是( )A、 B、 C、 D、7. 若 , 分别是一次函数图象上两个不相同的点,记 , 则为( )A、正数 B、负数 C、0 D、非负数8. 给定下列条件,不能判定三角形是直角三角形的是( )A、 B、 C、 D、9. 如图,一次函数与的图象相交于 , 则函数的图象可能是( ) A、
A、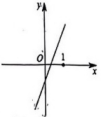 B、
B、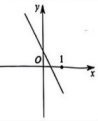 C、
C、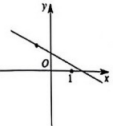 D、
D、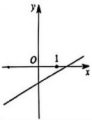 10. 如图,在中, , , 是边上一点,若为直角三角形,则的度数为( )
10. 如图,在中, , , 是边上一点,若为直角三角形,则的度数为( )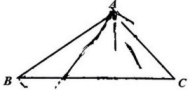 A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题(本大题共6小题,每小题3分,共18分)
-
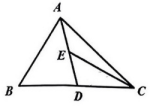
11. 点到轴的距离是 .12. 已知命题:“对顶角相等.”请写出它的逆命题: .13. 如图,已知中,是边上的中线,为的中点,若的面积为 , 则的面积为 .
 14. 函数的图象如图所示,则关于的不等式的解集为 .
14. 函数的图象如图所示,则关于的不等式的解集为 .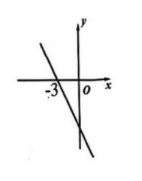 15. 在中, , 、是的内角平分线且相交于点 , 则 .16. 已知,在平面直角坐标系中,一次函数的图象经过 , .
15. 在中, , 、是的内角平分线且相交于点 , 则 .16. 已知,在平面直角坐标系中,一次函数的图象经过 , .⑴则该一次函数的解析式为;
⑵若直线与线段有公共点,则的取值范围为 .
三、解答题(本大题共7小题,共52分.请写出完整的解答或证明过程)
-
17. 已知与成正比例,当时, . 、(1)、求与之间的函数解析式;(2)、判断点是否在该函数图象上,并说明理由.18. 在中, , .(1)、求的取值范围;(2)、若的周长为偶数,求的周长为多少?19. 如图在平面直角坐标系中,已知 , , , 是的边上的一点,把经过平移后得 , 点、、的对应点分别为点、、 , 点的对应点为 .
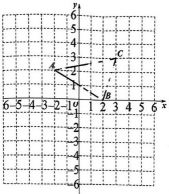 (1)、直接写出、、三个点的坐标并画出;(2)、求的面积.20. 求证:三角形的内角和等于 .21. 如图,已知一次函数和的图象交于点 , 这两个一次函数的图象与轴分别交于点、 .
(1)、直接写出、、三个点的坐标并画出;(2)、求的面积.20. 求证:三角形的内角和等于 .21. 如图,已知一次函数和的图象交于点 , 这两个一次函数的图象与轴分别交于点、 . (1)、分别求出这两个一次函数的表达式;(2)、求的面积;(3)、根据图象直接写出不等式的解集.22. 如图,在中, , 为边上的高,平分 , 分别交 , 于点 , .
(1)、分别求出这两个一次函数的表达式;(2)、求的面积;(3)、根据图象直接写出不等式的解集.22. 如图,在中, , 为边上的高,平分 , 分别交 , 于点 , . (1)、若 , 求的度数;(2)、与相等吗?请说明理由.23. 第19届亚运会已于2023年9月23日至10月8日在中国浙江杭州成功举行.这是党的二十大胜利召开之后我国举办的规模最大、水平最高的国际综合性体育赛事,举国关注,举世瞩目.杭州亚运会三个吉祥物分别取名“琮琮”“宸宸”“莲莲”.某专卖店购进A , B两种杭州亚运会吉祥物礼盒进行销售.A种礼盒每个进价160元,售价220元;B种礼盒每个进价120元,售价160元.现计划购进两种礼盒共100个,其中A种礼盒不少于60个.设购进A种礼盒x个,两种礼盒全部售完,该专卖店获利y元.(1)、求y与x之间的函数关系式;(2)、若购进100个礼盒的总费用不超过15000元,求最大利润为多少元?(3)、在(2)的条件下,该专卖店对A种礼盒以每个优惠元的价格进行优惠促销活动,B种礼盒每个进价减少n元,售价不变,且 , 若最大利润为4900元,请直接写出m的值.
(1)、若 , 求的度数;(2)、与相等吗?请说明理由.23. 第19届亚运会已于2023年9月23日至10月8日在中国浙江杭州成功举行.这是党的二十大胜利召开之后我国举办的规模最大、水平最高的国际综合性体育赛事,举国关注,举世瞩目.杭州亚运会三个吉祥物分别取名“琮琮”“宸宸”“莲莲”.某专卖店购进A , B两种杭州亚运会吉祥物礼盒进行销售.A种礼盒每个进价160元,售价220元;B种礼盒每个进价120元,售价160元.现计划购进两种礼盒共100个,其中A种礼盒不少于60个.设购进A种礼盒x个,两种礼盒全部售完,该专卖店获利y元.(1)、求y与x之间的函数关系式;(2)、若购进100个礼盒的总费用不超过15000元,求最大利润为多少元?(3)、在(2)的条件下,该专卖店对A种礼盒以每个优惠元的价格进行优惠促销活动,B种礼盒每个进价减少n元,售价不变,且 , 若最大利润为4900元,请直接写出m的值.