北师大版数学七年级上册期末冲刺满分攻略15 线的认识与线段长短比较
试卷更新日期:2024-01-02 类型:复习试卷
一、选择题
-
1. 如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
 A、过一点有无数条直线 B、两点之间线段的长度,叫做这两点之间的距离 C、经过两点有且只有一条直线 D、两点之间,线段最短2. 在墙壁上固定一根横放的木条,则至少需要( )枚钉子.A、1 B、2 C、3 D、随便多少枚3. 下列说法正确的是( )A、两点之间的连线中,直线最短 B、若P是线段AB的中点,则AP=BP C、若AP=BP,则P是线段AB的中点 D、两点之间的线段叫做这两点之间的距离4. 下列四个语句中,正确的是( )
A、过一点有无数条直线 B、两点之间线段的长度,叫做这两点之间的距离 C、经过两点有且只有一条直线 D、两点之间,线段最短2. 在墙壁上固定一根横放的木条,则至少需要( )枚钉子.A、1 B、2 C、3 D、随便多少枚3. 下列说法正确的是( )A、两点之间的连线中,直线最短 B、若P是线段AB的中点,则AP=BP C、若AP=BP,则P是线段AB的中点 D、两点之间的线段叫做这两点之间的距离4. 下列四个语句中,正确的是( )①如果线段AB=BC,则B是线段AC的中点;
②两点之间,直线最短;
③射线AB与射线BA表示同一条射线;
④如图,∠ABD也可用∠B表示.
 A、0个 B、1个 C、2个 D、3个5. 下列各种图形中,可以比较大小的是( )A、两条射线 B、两条直线 C、直线与射线 D、两条线段6. 由盘锦到沈阳的某一次列车,运行途中停靠的车站依次是:盘锦﹣西柳﹣海城﹣鞍山﹣辽阳﹣沈阳,那么要为这次列车制作的火车票有( )A、6种 B、12种 C、15种 D、30种7. 已知线段AB及一点P,如果PA+PB=AB,那么正确的是( )A、P为AB的中点 B、P在线段AB上 C、P在线段AB外 D、P在线段MN上8. 如图所示四幅图中,符合“射线PA与射线PB是同一条射线”的图为( )A、
A、0个 B、1个 C、2个 D、3个5. 下列各种图形中,可以比较大小的是( )A、两条射线 B、两条直线 C、直线与射线 D、两条线段6. 由盘锦到沈阳的某一次列车,运行途中停靠的车站依次是:盘锦﹣西柳﹣海城﹣鞍山﹣辽阳﹣沈阳,那么要为这次列车制作的火车票有( )A、6种 B、12种 C、15种 D、30种7. 已知线段AB及一点P,如果PA+PB=AB,那么正确的是( )A、P为AB的中点 B、P在线段AB上 C、P在线段AB外 D、P在线段MN上8. 如图所示四幅图中,符合“射线PA与射线PB是同一条射线”的图为( )A、 B、
B、 C、
C、 D、
D、 9. 如图,cm,为的中点,cm,则AB的长是( )
9. 如图,cm,为的中点,cm,则AB的长是( )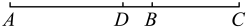 A、22cm B、17cm C、26cm D、4cm10. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( )
A、22cm B、17cm C、26cm D、4cm10. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( ) A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线
A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线二、填空题
-
11. 在数轴上点A、B表示的数分别是-3和5,则线段AB长是。12. 如图,已知线段 , 点C在线段上, , 则 .
 13. 工人师傅在用方砖铺地时,常常打两个木桩,然后沿着拉紧的线铺砖,这样地砖就铺得整齐,这个事实说明的原理是14. 如图,C、D为线段AB上的任意两点,那么图中共有条线段.
13. 工人师傅在用方砖铺地时,常常打两个木桩,然后沿着拉紧的线铺砖,这样地砖就铺得整齐,这个事实说明的原理是14. 如图,C、D为线段AB上的任意两点,那么图中共有条线段. 15. 平面内不同的两点确定一条直线,不同的三点最多确定三条直线,平面内不同的六个点最多可确定 条直线.16. 在一张零件图中,如图,已知 , , , 则 , .
15. 平面内不同的两点确定一条直线,不同的三点最多确定三条直线,平面内不同的六个点最多可确定 条直线.16. 在一张零件图中,如图,已知 , , , 则 , .
三、解答题
-
17. 如图,点C是线段外一点,用尺规作图作出下列图形(不写作法,但要保留作图痕迹);
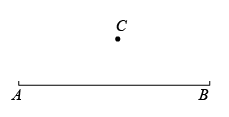
( 1 )作射线;
( 2 )作直线;
( 3 )延长线段到D点,使;
( 4 )在线段上找一点E,使 .
18. 在数轴上,如果A点表示的数记为a , 点B表示的数记为b , 则A、B两点间的距离可以记作|a-b|或|b-a|,我们把数轴上两点的距离,用两点的大写字母表示,如:点A与点B之间的距离表示为AB . 如图,在数轴上,点A , O , B表示的数为-10,0,12. (1)、直接写出结果,OA= , AB= .(2)、设点P在数轴上对应的数为x .
(1)、直接写出结果,OA= , AB= .(2)、设点P在数轴上对应的数为x .①若点P为线段AB的中点,则x= .
②若点P为线段AB上的一个动点,则|x+10|+|x-12|的化简结果是 .
(3)、动点M从A出发,以每秒2个单位的速度沿数轴在A , B之间向右运动,同时动点N从B出发,以每秒4个单位的速度沿数轴在A , B之间往返运动,当点M运动到B时,M和N两点停止运动.设运动时间为t秒,是否存在t值,使得OM=ON?若存在,请直接写出t值;若不存在,请说明理由.19. 结合数轴与绝对值的知识回答下列问题:数轴上表示和的两点之间的距离是 , 而;表示和两点之间的距离是 , 而;表示和两点之间的距离是 , 而 .
一般地,数轴上表示数和数的两点之间的距离公式为 .
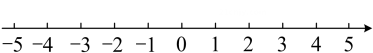 (1)、数轴上表示数的点与表示的点之间的距离为;(2)、数轴上表示数的点与表示的点之间的距离表示为 ;若数轴上位于与之间,求的值;(3)、如果表示数和的两点之间的距离是 , 则可记为: , 求的值.20. 如图,已知数轴上的点A表示的数为6,B是数轴上一点,且AB=10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)、数轴上表示数的点与表示的点之间的距离为;(2)、数轴上表示数的点与表示的点之间的距离表示为 ;若数轴上位于与之间,求的值;(3)、如果表示数和的两点之间的距离是 , 则可记为: , 求的值.20. 如图,已知数轴上的点A表示的数为6,B是数轴上一点,且AB=10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. (1)、写出点B表示的数 , 点P表示的数(用含t的代数式表示);(2)、动点R从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、R同时出发,点P运动几秒时追上点R,并求出此时P表示的数;(3)、若M为AP的中点,N为PB的中点点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,请求出线段MN的长.21. 线段AB上有一点M,在三条线段AB、AM和BM中,若有一条线段的长度是另一条线段长度的三分之一,则称点M是线段AB的“奇异点”.
(1)、写出点B表示的数 , 点P表示的数(用含t的代数式表示);(2)、动点R从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、R同时出发,点P运动几秒时追上点R,并求出此时P表示的数;(3)、若M为AP的中点,N为PB的中点点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,请求出线段MN的长.21. 线段AB上有一点M,在三条线段AB、AM和BM中,若有一条线段的长度是另一条线段长度的三分之一,则称点M是线段AB的“奇异点”.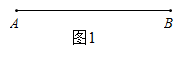
 (1)、如图1,线段厘米,若点是线段的“奇异点”,求AM的长.(2)、如图2,线段厘米,一个动点从点出发,以每秒3厘米的速度沿射线匀速运动.当点运动几秒时,点恰好是线段的“奇异点”?请说明理由.22. 在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴.上的对应点到原点的距离.而|5|=|5-0|,即|5-0|也可理解为5、0在数轴.上对应的两点之间的距离.类似的,|5-3|表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离,一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为|a-b|.
(1)、如图1,线段厘米,若点是线段的“奇异点”,求AM的长.(2)、如图2,线段厘米,一个动点从点出发,以每秒3厘米的速度沿射线匀速运动.当点运动几秒时,点恰好是线段的“奇异点”?请说明理由.22. 在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴.上的对应点到原点的距离.而|5|=|5-0|,即|5-0|也可理解为5、0在数轴.上对应的两点之间的距离.类似的,|5-3|表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离,一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为|a-b|.
请根据绝对值的意义并结合数轴解答下列问题:
(1)、数轴上表示2和3的两点之间的距离是;数轴上表示和-5的两点之间的距离是(2)、数轴上点P表示的数是2,P、Q两点的距离为3,则点Q表示的数是(3)、|x+|的几何意义是数轴上表示有理数的点与表示x的点之间的距离;(4)、若|m-3|+|m+2|=7,则m=(5)、数轴上有一个点表示数a,则|a+1|+|a-3|+|a+8|的最小值为23. 阅读下面材料:①在数轴上,有理数5与-2对应两点间的距离为|5-(-2)|=7;
②在数轴上,有理数-2与3对应两点之间的距离为|-2-3|=5;
③在数轴上,有理数-8与-5对应两点之间的距离为|-8-(-5)|=3;
④在数轴上点A、B分别表示数a,b,则A、B两点之间的距离AB=|a-b|;

回答下列问题:
(1)、①在数轴上表示-2与-5两点间的距离为是 ,
②在数轴上表示x与3两点间的距离为距离是;
③在数轴上表示x与两点之间的距离为|x+1|(2)、下面对式子|x+1|+|x-3|进行探究:①当表示数x的点在-1与3之间移动时,|x+1|+|x-3|的值总是一个固定的值为:。
②要使|x+1|+|x-3|=8,数轴上表示的数x=.
(3)、|x-3|+|x-2|+|x+1|+|x+2|的最小值:.24. 已知点A在数轴上对应的数为a , 点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A、B之间的距离记为|AB|=|a-b|或|b-a|,请回答问题:(1)、直接写出a , b,|AB|的值,a= , b= , |AB|=(2)、设点P在数轴上对应的数为x , 若|x-3|=5,则x=(3)、如图,点M.N,P是数轴上的三点,点M表示的数为4,点N表示的数为-1,动点P表示的数为x.
①若点P在点M、N之间,则|x+1|+|x-4|= ▲
②若|x+1|+|x-4|=10,则x= ▲
③若点P表示的数是-5,现在有一蚂蚁从点P出发,以每秒1个单位长度的速度向右运动,当经过多少秒时,蚂蚁所在的点到点M、点N的距离之和是8?