北师大版数学七年级上册期末冲刺满分攻略14 探索数与式的规律

试卷更新日期：2024-01-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，是一组有规律的图案，它们是由边长相同的小正方形组成的，其中部分小正方形涂有阴影，按照这样的规律，第2023个图案中涂有阴影的小正方形个数是（）

A、 $10110$ B、 $10115$ C、 $8092$ D、 $8093$

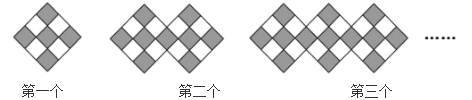查看试题解析
2. 我国宋朝时期的数学家杨辉，曾将大小完全相同的圆弹珠逐层堆积，形成“三角垛”；图2有3颗弹珠；图3有6颗弹珠，第5个图，…；若用a_n表示图n的弹珠数，其中n＝1，2，3，…，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + … + \frac{1}{a_{2023}}$ ＝（）

A、 $\frac{4044}{2023}$ B、 $\frac{4042}{2023}$ C、 $\frac{2021}{1011}$ D、 $\frac{2023}{1012}$

查看试题解析
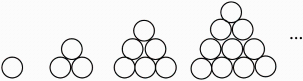3. 计算机利用的是二进制数，它共有两个数码0，1，将一个十进制数转化为二进制，只需将该数写为若干个2ⁿ的数字之和，依次写出1或0的系数即可，如十进制数字19可以写为二进制数字10011，因为19=16+2+1=1×2⁴+0×2³+0×2²+1×2¹+1×2⁰ ， 32可以写为二进制数字100000，因为32＝32＝1×2⁵+0×2⁴+0×2³+0×2²+0×2¹+0×2⁰ ，则十进制数字70是二进制下的（）

A、4位数 B、5位数 C、6位数 D、7位数

查看试题解析
4. 如图，将一个边长为1的正方形纸片分割成7个部分，部分①是整体面积的一半，部分②是部分①面积的一半，依次类推，则 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdot \cdot \cdot + \frac{1}{2^{6}}$ 的值是（）

A、 $\frac{15}{16}$ B、 $\frac{31}{32}$ C、 $\frac{63}{64}$ D、 $\frac{127}{128}$

查看试题解析
5. 面食不仅是中华民族饮食文化的重要组成部分，也是世界的面食之根其中，“拉面”远播世界各地，制作方法是：用一根很粗的面条，把两头捏合在一起拉伸，再捏合，反复几次，这根很粗的面条就被拉成许多细的面条，第一次捏合变 $2$ 根细面条，第二次捏合变 $4$ 根细面条，第三次捏合变 $8$ 根细面条，这样捏合到第 $n$ 次后可拉出细面条（）

A、 $2^{n - 1}$ 根 B、 $2^{n}$ 根 C、 $2^{n + 1}$ 根 D、 $(\frac{1}{2})^{n + 1}$ 根

查看试题解析
6. 如图所示，动点 $P$ 从第一个数0的位置出发，每次跳动一个单位长度，第一次跳动一个单位长度到达数1的位置，第二次跳动一个单位长度到达数2的位置，第三次跳动一个单位长度到达数3的位置，…，依此规律跳动下去，点 $P$ 从0跳动6次到达 $P_{1}$ 的位置，点点 $P$ 从0跳动21次到达 $P_{2}$ 的位置，…，点 $P_{1} 、 P_{2} 、 P_{3} \cdot \cdot \cdot P_{n}$ 在一条直线上，则点 $P$ 从0跳动（）次可到达 $P_{12}$ 的位置．

A、595 B、666 C、630 D、703

查看试题解析
7. 如图所示运算程序中，若开始输入的x值为48，第一次输出的结果为24，第二次输出的结果为12，……，则第2021次输出的结果是（）

A、1 B、6 C、3 D、4

查看试题解析
8. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和，如： $2^{3} = 3 + 5$ ， $3^{3} = 7 + 9 + 11$ ， $4^{3} = 13 + 15 + 17 + 19$ ， …按此规律，若 $m^{3}$ 分裂后，其中有一个奇数是2023，则m的值是（）

A、46 B、45 C、44 D、43

查看试题解析
9. 正六边形ABCDEF在数轴上的位置如图，点A、F对应的数分别为0和1，若正六边形ABCDEF绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点E所对应的数为2，则连续翻转2021次后，数轴上2021这个数所对应的点是（）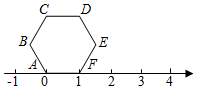

A、A点 B、B点 C、C点 D、D点

查看试题解析
10. 一组数据排列如下：
1

2 3 4

3 4 5 6 7

4 5 6 7 8 9 10

…

按此规律，某行最后一个数是148，则此行的所有数之和是（）

A、9801 B、9603 C、9025 D、8100

查看试题解析

二、填空题

11. 将正整数按如图所示的位置顺序排列，根据排列顺序，2023应在点处．

查看试题解析
12. 已知 $x_{1} ， x_{2} ， x_{3} ， ⋯ ， x_{20}$ 都是非零有理数，若 $y_{1} = \frac{| x_{1} |}{x_{1}}$ ，则 $y_{1}$ 等于1或 $- 1$ ；若 $y_{2} = \frac{| x_{1} |}{x_{1}} + \frac{| x_{2} |}{x_{2}}$ ，则 $y_{2}$ 等于2或 $- 2$ 或0；若 $y_{20} = \frac{| x_{1} |}{x_{1}} + \frac{| x_{2} |}{x_{2}} + \frac{| x_{3} |}{x_{3}} + ⋯ + \frac{| x_{20} |}{x_{20}}$ ，则 $y_{20}$ 所有可能等于的值的绝对值之和等于．

查看试题解析
13. 化学中直链烷烃的名称用“碳原子数+烷”来表示，当碳原子数为 $1 ~ 10$ 时，依次用天干——甲、乙、丙、丁、戊、己、庚、辛、王、癸表示，其中甲烷、乙烷、丙烷的分子结构式如图所示，则第7个庚烷分子结构式中“ $H$ ”的个数是．

查看试题解析
14. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动，第1次将点A向左移动3个单位长度到达点A₁ ，第2次将点A₁向右平移6个单位长度到达点A₂ ，第3次将点A₂向左移动9个单位长度到达点A₃…则第6次移动到点A₆；按照这种规律移动下去，至少移动次后该点到原点的距离不小于41．

查看试题解析
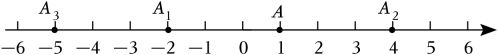15. 如图，下列图案是由火柴棒按某种规律搭成的，第(1)个图案中有2个正方形，第(2)个图案中有5个正方形，第(3) 个图案中有8个正方形……则第n个图案中有个正方形．

查看试题解析
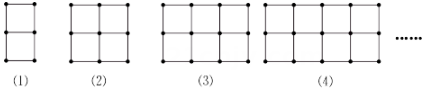16. 一组数据按如下规律排列： $a_{1} = 1 \times 2 \times 3$ ， $a_{2} = 2 \times 3 \times 4$ ， $a_{3} = 3 \times 4 \times 5$ ， ……．如果 $\frac{3 m}{a_{8}} = \frac{1}{a_{8}} - \frac{1}{a_{7}}$ ，那么 $m =$ ．

查看试题解析

三、计算题

17. 阅读下列内容，然后解答问题：
因为： $\frac{1}{1 \times 2} = 1 - \frac{1}{2} ， \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ， \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4} \dots \frac{1}{9 \times 10} = \frac{1}{9} - \frac{1}{10}$

所以： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{9 \times 10}$

$= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \dots + (\frac{1}{9} - \frac{1}{10})$

$= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \dots + \frac{1}{9} - \frac{1}{10}$

$= 1 - \frac{1}{10} = \frac{9}{10}$

问题：计算：

(1)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2015 \times 2016} + \frac{1}{2016 \times 2017}$

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7}$

(3)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{2015 \times 2017}$

查看试题解析
18. 将正整数1，2，3，4，5，6，7，…，排成如图所示的数表．

(1)、根据规律，数24位于第4行第3列，那么数100位于第行第列；

(2)、数表中第n行第1列的数是，并求出第n行所有数的和（用含n的式子表示）；

(3)、如图，“T”字型分别框出一横行左右相邻的三个数和一竖列上下相邻的三个数，容易求出横行三个数的和与竖列三个数的和，分别记为 $S_{1} ， S_{2}$ ．
①猜想 $S_{1} ， S_{2}$ 之间的关系 ▲ ；
②任意平移“T”字型的位置， $S_{1}$ 与 $S_{2}$ 之间的关系还成立吗？若成立，请通过计算说明理由；若不成立，请举例说明．

查看试题解析
19. 如图，半径为1的小圆与半径为2的大圆上有一点与数轴上原点重合，两圆在数轴上做无滑动的滚动，小圆的运动速度为每秒π个单位，大圆的运动速度为每秒2π个单位．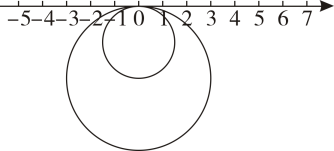

(1)、若大圆沿数轴向左滚动1周，则该圆与数轴重合的点所表示的数是；

(2)、若小圆不动，大圆沿数轴来回滚动，规定大圆向右滚动时间记为正数，向左滚动时间记为负数，依次滚动的情况记录如下(单位：秒) ：-1，+2，-4，-2，+3，-8
①第次滚动后，大圆离原点最远？
②当大圆结束运动时，大圆运动的路程为？此时两圆与数轴重合的点之间的距离是？(结果保留π)

(3)、若两圆同时在数轴上各自沿着某一方向连续滚动，滚动一段时间后两圆与数轴重合的点之间相距9π，求此时两圆与数轴重合的点所表示的数．

查看试题解析
20. 将图1中的菱形剪开得到图2，则图2中共有4个菱形；将图2中的一个菱形剪开得到图3，则图3中共有7个菱形，…如此剪下去，请结合图形解决问题

(1)、按图示规律填写下表：
图
1
2
3
4
5
…
菱形个数
1
4
7
…

(2)、按照这种方式剪下去，则第n个图中共有个菱形．

(3)、按照这种方式剪下去，则第2017个图中共有个菱形．

查看试题解析
21. 阅读下列材料：
① $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ $⋯$
② $\frac{1}{1 \times 3} = \frac{1}{2} \times (1 - \frac{1}{3})$ ， $\frac{1}{3 \times 5} = \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5})$ ， $\frac{1}{5 \times 7} = \frac{1}{2} \times (\frac{1}{5} - \frac{1}{7})$ $⋯$
③ $\frac{1}{1 \times 4} = \frac{1}{3} \times (1 - \frac{1}{4})$ ， $\frac{1}{4 \times 7} = \frac{1}{3} \times (\frac{1}{4} - \frac{1}{7})$ ， $\frac{1}{7 \times 10} = \frac{1}{3} \times (\frac{1}{7} - \frac{1}{10})$ $⋯$

(1)、写出①组中的第6个等式：，第n个等式：；

(2)、写出②组的第n个等式：；

(3)、利用由①②③组中你发现的等式规律计算：
$\frac{2}{1 \times 5} + \frac{2}{5 \times 9} + \frac{2}{9 \times 13} + ⋯ + \frac{2}{405 \times 401}$ ．

查看试题解析
22. 阅读下面材料：
在计算 $2 + 5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29$ 时，我们发现，从第一个数开始，后面的每个数与它的前面一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外我们还可以用下面的分式来计算，设它的和为 $S$ ，则 $S = \frac{n \cdot (a_{1} + a_{n})}{2}$ （其中 $n$ 表示数的个数， $a_{1}$ 表示第一个数， $a_{n}$ 表示最后一个数），那么 $2 + 5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 = \frac{10 \times (2 + 29)}{2} = 155$ .
用上面的知识解答下面的问题
某集团公司决定将下属的一个分公司对外招商，有符合条件的两家企业 $A$ 、 $B$ 分别拟定上缴利润方案如下：
$A$ ：每年结算一次上缴利润，第一年上缴利润 $1$ 万元，以后每年比前一年增加 $1$ 万元.
$B$ ：每半年结算一次上缴利润，第一个半年上缴 $0.3$ 万元，以后每半年比前半年增加 $0.3$ 万元.

(1)、如果承包 $4$ 年，你认为应该由哪家企业承包，总公司获利多？

(2)、如果承包 $n$ 年，请用含 $n$ 的式子分别表示两家企业上缴的总金额（单位：万元）.

查看试题解析
23. 探究题．
用棋子摆成的“T”字形图如图所示：

(1)、填写表：
图形序号
①
②
③
④
…
⑩
每个图案中棋子个数
5
8
…

(2)、写出第n个“T”字形图案中棋子的个数（用含n的代数式表示）；

(3)、第20个“T”字形图案共有棋子多少个？

(4)、计算前20个“T”字形图案中棋子的总个数．（提示：请你先思考下列问题：第1个图案与第20个图案中共有多少个棋子？第2个图案与第19个图案中共有多少个棋子？第3个图案与第18个图案呢？）

查看试题解析
24. 观察下列数表

根据数表反映的规律，猜想第6行与第6列的交叉点上的数应为多少．

(1)、第n行与第n列的交叉点上的数应为多少．（用含正整数n的式子表示）

(2)、计算左上角2×2的正方形里所有数字之和，即： $\begin{matrix} 1 \\ - 2 \end{matrix}$ $\begin{matrix} - 2 \\ 3 \end{matrix}$ 在数表中任取几个2×2的正方形，计算其中所有数字之和，归纳你得出的结论．

查看试题解析

图形序号	①	②	③	④	…	⑩
每个图案中棋子个数	5	8			…

图	1	2	3	4	5	…
菱形个数	1	4	7			…