北师大版数学七年级上册期末冲刺满分攻略13 整式的认识及其运算

试卷更新日期：2024-01-01 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知a ， b ， c在数轴上对应的点如图所示，则代数式 $| b - a | - | c + b | + | a - c |$ 化简后的结果为（）

A、 $2 b - 2 c$ B、 $2 b + 2 a$ C、2b D、 $- 2 a$

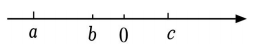查看试题解析
2. 如果a和-4b互为相反数，那么多项式2(-b-2a+10)+3(a+2b-3)的值是（）

A、11 B、29 C、0 D、9

查看试题解析
3. 两艘船从同一港口出发，甲船顺水而下，乙船逆水而上，已知两船在静水中的速度都是45km/h，水流速度是akm/h，1h后两船相距（）km.

A、90 B、4a C、2a D、180

查看试题解析
4. 把多项式x³-xy²+x²y+x⁴-3按x的降幂排列是( )

A、x⁴+x³+x²y-3-xy² B、-xy²+x²y+x⁴+x³-3 C、-3-xy²+x²y+x³+x⁴ D、x⁴+x³+x²y-xy²-3

查看试题解析
5. 若单项式 $a^{m + 3} b^{2}$ 与 $\frac{1}{2} a b^{n}$ 是同类项，则 $m n$ 的值是（）

A、-6 B、-4 C、9 D、4

查看试题解析
6. 下列运算结果不正确的有（）
①2a+b=2ab；②4a²-a²=3；③-x²-x²=-2x²；④5mn-5n=m

A、1个 B、2个 C、3个 D、4个

查看试题解析
7.
下图是一个数值转换机，若输入的x为–7，则输出的结果是（）

A、12 B、-14 C、27 D、21

查看试题解析
8.
如图1，将一个边长为a的正方形纸片剪去两个矩形，得到一个“S”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为（　　）

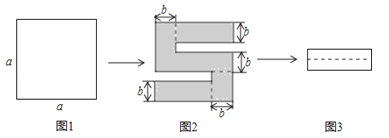A、2a﹣3b B、2a﹣4b C、4a﹣8b D、4a﹣10b

查看试题解析
9. 下列说法中，不正确的是（）

A、若a和b都是负数，且|a|＞|b|，则a＜b B、-2xyz³的系数是-2，次数是5 C、若a和b都是正数，且|a|＞|b|，则a＞b D、πd+2πR是二次二项式

查看试题解析
10. 代数式 $\frac{1}{x}$ ， 2x+y ， $\frac{1}{3}$ a²b ， $\frac{x - y}{π}$ ， 0.5， $\frac{5 y}{4 x}$ 中整式的个数为（　　）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 若多项式x^|^m^-3|-8x²+（m-7）x是关于x的四次三项式，则m的值为．

查看试题解析
12. 长为3m+2n，宽为5m﹣n的长方形的面积为

查看试题解析
13. 化简-x²+x-2-（-x²+1）= ．

查看试题解析
14. 定义一种新运算：a※b= $\{\begin{matrix} a - b (a \geq b) \\ 3 b (a < b) \end{matrix}$ ，则当x=3时，2※x﹣4※x的结果为

查看试题解析
15. 已知a ， b ， c在数轴上的位置如图所示，则 $| a + b | - | c - b | + | b - a |$ =

查看试题解析
16. 如图，将边长为4的正方形和半径为2的圆叠放在一起，两个空白部分的面积分别为m，n（m＞n），则m-n的值为（结果保留π）．

查看试题解析

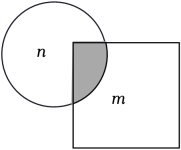
三、解答题

17. 化简：

(1)、 $2 x^{2} + 1 - 3 x + 7 - 2 x^{2} + 5 x$ ；

(2)、 $4 (x^{2} - x y + 6) - 3 (2 x^{2} + x y)$

查看试题解析
18. 已知代数式 $A = 3 x^{2} y^{2} + x y - 1$ ，代数式 $B = - x^{2} y^{2} - 2 y + 1$ ，代数式 $C = 2 A - (A - 3 B)$ .

(1)、化简代数式C；

(2)、若代数式C的值与y的取值无关，求x的值.

查看试题解析
19. 如图，长为 $a$ ，宽为 $b$ 的长方形被分割成7个部分，除两个阴影图形M，N外，其余的5个部分为形状和大小完全相同的小长方形，其中小长方形的宽为3.

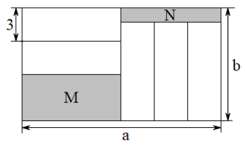(1)、求小长方形的长（用含 $a$ 的代数式表示）；

(2)、希望小组的同学们发现阴影图形M和阴影图形N的周长之和与 $a$ 的值无关，希望小组的判断是否正确，请说明理由.

查看试题解析
20. 如图，已知数轴上两点A、B.点C为数轴上的动点，其表示的数为x.

(1)、若点C到点A、B的距离相等，则点C表示的数x的值为；

(2)、式子|x-3|+|x+1|的最小值是；

(3)、点D也是数轴上的一个动点，已知点C的运动速度为每秒2个单位长度，动点C、D同时分别从点A、B出发开始运动.
①若点C、D相向而行，在表示数 $\frac{3}{5}$ 的点相遇，求点D的运动速度；
②若点D的运动速度是每秒4个单位长度，C、D两点同时向左匀速运动，则当C、D两点之间的距离为2时，两点运动了多长时间?

(4)、若动点C从点A出发，第一次向左运动1个单位长度，第二次向右运动2个单位长度，第三次向左运动3个单位长度，…，按此规律不断在数轴上做往复运动，当点C运动了n次时，直接用含n的代数式表示出点C所表示的有理数.

查看试题解析
21. 将连续的奇数1，3，5，7，9…排成如图所示的数阵，用十字框按如图所示的方式任意框五个数.（十字框只能平移）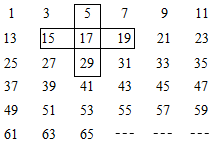

(1)、若框住的5个数中，正中间的一个数为17，则这5个数的和为.

(2)、设正中间的数为a ，用式子表示十字框内五个数的和.

(3)、十字框能否框住这样的5个数，它们的和等于2035？若能，求出正中间的数a；若不能，请说明理由.

查看试题解析
22. 某公司生产一种电子产品和配件，已知该电子产品的售价为200元/台，配件的售价为20元/个，在促销活动期间，有如下两种优惠方案（顾客只能选择其中一种优惠方案）：
①买一台电子产品送一个配件；
②电子产品每台降价10元出售，配件每个打9折.
在促销活动期间，某学校计划到该公司购买 $x$ 台电子产品， $y$ 个配件 $(y > x > 0)$ .

(1)、分别求该校选择优惠方案①，②购买该电子产品和配件所需的总费用；（用含x、y的代数式来表示）

(2)、若该校计划购买该电子产品10台，配件20个，请通过计算判断，选择哪种优惠方案更省钱？

查看试题解析
23.

(1)、阅读材料：我们知道，4x+2x-x=（4+2-1）x=5x ，类似地，我们把（a+b）看成一个整体，则4(a+b)+2(a+b)-(a+b)=(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛。
尝试应用：
①把(a+b)²看成一个整体，合并-3(a+b)²-6(a+b)²+8(a+b)²的结果 ▲ .
②拓广探索：已知a-2b=5，2b-c=-7，c-d=12，求4(a-c)+4(2b-d)-4(2b-c)的值.

(2)、某人用400元购买了8套电子产品，准备以一定价格出售，如果每套电子产品以56元的价格作为标准卖出，超出的记为正数，不足的记为负数，记录如下（单位：元）：
-3，+7，-8，+9，-2，0，-1，-6，
当他卖完这8套电子产品后是盈利还是亏损？

查看试题解析
24. 阅读材料，回答问题．
材料一：因为2³=2×2×2，2²=2×2，所以2³×2²=(2×2×2)×(2×2)=25.
材料二：求3¹+3²+3³+3⁴+3⁵+3⁶的值.
解：设S=3¹+3²+3³+3⁴+3⁵+3⁶①
则3S=3²+3³+3⁴+3⁵+3⁶+3⁷②
用②－①得，3S－S=(3²+3³+3⁴+3⁵+3⁶+3⁷)－(3¹+3²+3³+3⁴+3⁵+3⁶)=3⁷－3
所以2S=3⁷－3，即S= $\frac{3^{7} － 3}{2}$
所以3¹+3²+3³+3⁴+3⁵+3⁶= $\frac{3^{7} － 3}{2}$
这种方法我们称为"错位相减法".

(1)、填空：5×5⁸=5^（^）， a²·a⁵=a^（^）.

(2)、"棋盘摆米"是一个著名的数学故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏．阿基米德对国王说："我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行"国王以为要不了多少粮食，就随口答应了．
①国际象棋共有64个格子，则在第64格中应放 ▲ 粒米．（用幂表示）
②设国王输给阿基米德的总米粒数为S，求S.

查看试题解析