北师大版数学七年级上册期末冲刺满分攻略12 代数式的认识及其求值

试卷更新日期：2023-12-29 类型：复习试卷

进入出卷网下载

一、选择题

1. 当 $x = 2$ 时， $a x^{3} + b x + 1 = 6$ ，那么当 $x = - 2$ 时， $a x^{3} + b x + 1$ 值是（）

A、 $1$ B、 $- 4$ C、 $6$ D、 $- 5$

查看试题解析
2. 我国宋朝时期的数学家杨辉，曾将大小完全相同的圆弹珠逐层堆积，形成“三角垛”；图2有3颗弹珠；图3有6颗弹珠，第5个图，…；若用a_n表示图n的弹珠数，其中n＝1，2，3，…，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + … + \frac{1}{a_{2023}}$ ＝（）

A、 $\frac{4044}{2023}$ B、 $\frac{4042}{2023}$ C、 $\frac{2021}{1011}$ D、 $\frac{2023}{1012}$

查看试题解析
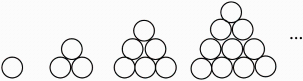3. 一个长方形的长为x ，宽比长的一半多1，则这个长方形的面积为（）

A、 $2 x^{2} + 2 x$ B、 $2 x^{2} - 2 x$ C、 $\frac{1}{2} x^{2} + x$ D、 $\frac{1}{2} x^{2} - x$

查看试题解析
4. 如图是一块长为a，宽为b（a＞b）的长方形空地，要将阴影部分绿化，则阴影面积是（）

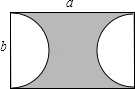A、a²b² B、ab﹣πa² C、 $a b - \frac{π}{4} b^{2}$ D、 $a b - \frac{π}{4} a^{2}$

查看试题解析
5. 欢欢从山脚登上山顶共用时5h，其中2h的速度为v₁km/h，另外3h的速度为v₂km/h，欢欢再以 $\frac{v_{1} + v_{2}}{2}$ km/h的速度沿原路下山。如果v₁<v₂ ，那么欢欢返回山脚的用时（）

A、刚好5h B、不到5h C、超过5h D、不能确定

查看试题解析
6. 代数式2a²+3a+1的值是6，那么代数式6a²+9a+5的值是（）

A、20 B、18 C、16 D、15

查看试题解析
7. 下列结论中，正确的是（）

A、代数式πx²+4x-3是三次三项式 B、3x²y与-2xy²是同类项 C、代数式x²+4x-3的常数项是3 D、单项式- $\frac{3 x^{2} y}{5}$ 系数是- $\frac{3}{5}$ ，次数是3

查看试题解析
8. 代数式 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{a b}{| a b |}$ 的所有可能的值有（）

A、 $2$ 个 B、 $3$ 个 C、 $4$ 个 D、无数个

查看试题解析
9. 用代数式表示“2m与5的差”为（）

A、5－2m B、2m－5 C、2(m－5) D、2(5－m)

查看试题解析
10. 若代数式y²-2y+1的值是5，则代数式2y²-4y-5的值是（）

A、-3 B、25 C、-25 D、3

查看试题解析

二、填空题

11. 若（2x+1）²+|y-1|＝0，则x²+y²的值是．

查看试题解析
12. 某种水果的售价为每千克a元，用面值为50元的人民币购买了3千克这种水果，应找回元（用含a的代数式表示）．

查看试题解析
13. 如图所示的运算程序中，若开始输入的x值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，第2022次输出的结果为．

查看试题解析
14. 某企业去年产值x万元，今年比去年增产10%，今年产值是万元．

查看试题解析
15. 某服装店将原来每件m元的服装加价50%后销售，由于转季，服装店将该服装降价40%，则经过降价后每件服装的价格为元（结果用含m的代数式表示）．

查看试题解析
16. 把两个边长分别为a（a＜4）和4的正方形按如图的式样摆放，则图中阴影部分的面积为．

查看试题解析

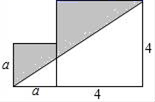
三、计算题

17. 代数式求值：

(1)、求代数式3x²+3xy-9的值，其中x=2，y=-3．

(2)、已知|a|=3，|b-5|=5，且a>b，求a+b的值．

查看试题解析
18. 在代数式求值问题中，整体思想运用十分广泛，如：已知代数式5a+3b＝-4，求代数式2（a+b）+4（2a+b）+3的值．解法如下：
原式＝2a+2b+8a+4b+3＝10a+6b+3＝2（5a+3b）+3＝2×（-4）+3＝-5．
利用整体思想，完成下面的问题：

(1)、已知-m²＝m ，则m²+m+1＝；

(2)、已知m-n＝2，求2（n-m）-4m+4n-3的值．

(3)、已知m²+2mn＝-2，mn-n²＝-4，求 $3 m^{2} + \frac{9}{2} m n + \frac{3}{2} n^{2}$ 的值．

查看试题解析
19. 如图，在一个底为a ，高为h的三角形铁皮上剪去一个半径为r的半圆．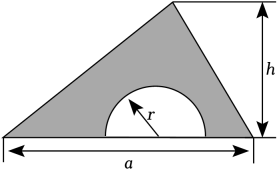

(1)、用含a ， h ， r的代数式表示剩下铁皮（阴影部分）的面积S ．

(2)、请求出当a＝10，h＝8，r＝2时（结果保留π）．

查看试题解析
20. 某同学绘制了如图所示的火箭模型截面图，图的下面是梯形，中间是长方形，上面是三角形．

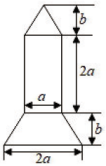(1)、用含有 $a 、 b$ 的代数式表示该截面的面积 $S$ ；

(2)、当 $a = 2.8 c m ， b = 2.2 c m$ 时，求这个截面的面积．

查看试题解析
21. 某校准备购买篮球50个，跳绳 $x$ 条 $(x > 50)$ ．篮球定价80元/个，跳绳定价20元/条．商店甲、乙向学校提供了各自的优惠方案：
商店甲：买一个篮球送一条跳绳；
商店乙：篮球和跳绳都按定价的 $90 %$ 付款．

(1)、若该校到商店甲、乙购买，分别需付款多少元；（用含 $x$ 的代数式表示）

(2)、若 $x = 300$ ，通过计算说明此时哪间商店购买较为合算？

(3)、当 $x = 300$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并把付款的钱算出来．

查看试题解析
22. 阅读材料，回答问题．
我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ ． “整体思想”是中学教学课题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．

(1)、尝试应用：把 $(a - b)^{2}$ 看成一个整体，合并 $3 (a - b)^{2} - 5 (a - b)^{2} + 7 (a - b)^{2}$ 的结果是；

(2)、已知 $2 x^{2} - 3 y = 6$ ，求 $- 4 x^{2} + 6 y - 5$ 的值；

(3)、拓展探索：已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(2 a - c) + (2 b - 3 d) - (4 b - 3 c)$ 的值．

查看试题解析
23. 小华在学习了整式一章中的字母表示数的内容后，对用字母表示规律产生了浓厚的兴趣，他用完全相等的小木棒搭建了如图所示的四个图形．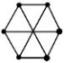

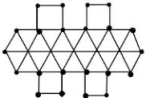
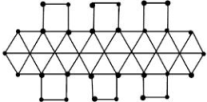
图1 图2 图3 图4

(1)、观察图形，其中图1用了根小木棒，图2用了根小木棒，图3用了根小木棒；

(2)、若按小华的方式继续搭建，猜想第n个图形中，小木棒的根数是多少？

(3)、根据（2）中的猜想，当 $n = 300$ 时，用了多少根小木棒？

查看试题解析
24. 综合与实践
【问题情境】如图，现有一张边长为20cm的正方形废弃宣传单，小华准备将其四个角各剪去一个小正方形，折成无盖长方体形纸盒．

(1)、【操作探究】剪去的小正方形的边长按整数值依次变化，即分别取1cm，2cm，3cm，4cm，5cm，6cm，7cm，8cm，9cm，10cm时，折成的无盖长方体的容积分别是多少？请你将计算的结果填入下表；
剪去正方形的边长/cm
1
2
3
4
5
6
7
8
9
10
容积 $/ c m^{3}$
324
512
500
384
252
128
36
0

(2)、【操作分析】观察绘制的统计表，你发现，随着减去的小正方形的边长的增大，所折无盖长方体盒子的容积如何变化？____

A、一直增大 B、一直减小 C、先增大后减小 D、先减小后增大

(3)、分析猜想当剪去图形的边长为cm时，所得的无盖长方体的容积最大，此时无盖长方体的容积是 $c m^{3}$ ．

(4)、【操作反思】对（1）中的结果，你觉得表格中的数据还有什么要改进的地方吗？

查看试题解析

剪去正方形的边长/cm	1	2	3	4	5	6	7	8	9	10
容积 $/ c m^{3}$	324	512			500	384	252	128	36	0