2023-2024学年苏科版数学八年级上册期末考试仿真模拟试卷
试卷更新日期:2023-12-29 类型:期末考试
一、选择题(每题3分,共24分)
-
1. 不属于( )A、无理数 B、负数 C、分数 D、实数2. 点到原点的距离为( )A、 B、 C、 D、3. 16的算术平方根是( )A、16 B、4 C、﹣4 D、±44. 下列条件中,不能判定两个直角三角形全等的是( )A、一锐角和斜边对应相等 B、两条直角边对应相等 C、斜边和一直角边对应相等 D、两个锐角对应相等5. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、
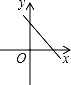 B、
B、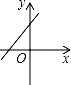 C、
C、 D、
D、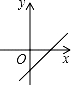 6. 已知点和点都在上,则和大小关系为( )A、 B、 C、 D、无法确定7. 对于试题“在中, , 过点A作 , 求使恰好把分成两个等腰三角形时的条件”,甲乙丙三人的说法如下:
6. 已知点和点都在上,则和大小关系为( )A、 B、 C、 D、无法确定7. 对于试题“在中, , 过点A作 , 求使恰好把分成两个等腰三角形时的条件”,甲乙丙三人的说法如下:甲:;乙: , ;丙:.
下面说法正确的是( )
A、甲说法正确 B、甲、乙说法正确 C、甲、乙、丙说法都正确 D、三种说法都正确但不全面8. 如图,一次函数与的图像交于点P,下列结论:①;②;③当时,;④;⑤ . 所有正确结论的序号为( ).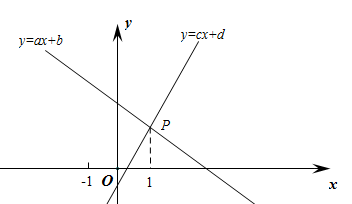 A、①②③ B、①②④ C、②③⑤ D、②④⑤
A、①②③ B、①②④ C、②③⑤ D、②④⑤二、填空题(每题3分,共30分)
-
9. 7的算术平方根是 .10. 计算: = .11. 209506精确到千位的近似值是 .12. 比较大小:-2.(填“>”或“<”)13. 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、2、3、4,则最大的正方形E的面积是 .
 14. 如图,已知Rt△ABC , AB=AC , 将边AB绕着点A旋转,当点B落在边AB的垂直平分线上的点E时,∠AEC=.
14. 如图,已知Rt△ABC , AB=AC , 将边AB绕着点A旋转,当点B落在边AB的垂直平分线上的点E时,∠AEC=. 15. 在一张边长为的正方形纸片上剪下一个一边长为的等腰三角形,要求:等腰三角形的三个顶点都落在正方形的边上,且其中一个顶点与正方形的顶点重合,则所得等腰三角形的面积可能是(写出至少三个)
15. 在一张边长为的正方形纸片上剪下一个一边长为的等腰三角形,要求:等腰三角形的三个顶点都落在正方形的边上,且其中一个顶点与正方形的顶点重合,则所得等腰三角形的面积可能是(写出至少三个) 16. 已知一次函数y= x+1的图象与y轴交于点A,将该函数图象绕点A旋转45°,旋转后的图象对应的函数关系式是.17. 如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 cm/s时,能够使△BPE与△CQP全等.
16. 已知一次函数y= x+1的图象与y轴交于点A,将该函数图象绕点A旋转45°,旋转后的图象对应的函数关系式是.17. 如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 cm/s时,能够使△BPE与△CQP全等. 18. 已知一次函数(为常数, , 若当时有 , 则的取值范围是.
18. 已知一次函数(为常数, , 若当时有 , 则的取值范围是.三、解答题(共8题,共66分)
-
19. 求下列各式中的:(1)、 .(2)、 .20. 如图,已知△BAC和△DAE的顶点A重合,∠BAC=∠DAE , AB=AC , AD=AE , 连接BD、CE交于点M .
 (1)、证明:∠ABD=∠ACE;(2)、若∠BAC=70°,求∠BMC的大小.21. 已知,点 , , .
(1)、证明:∠ABD=∠ACE;(2)、若∠BAC=70°,求∠BMC的大小.21. 已知,点 , , . (1)、在坐标系中画出;(2)、求的面积;(3)、画出关于x轴的对称图形 , 并写出点 , , 的坐标.22. 如图,△ABC的三边分别为AC=6,BC=8,AB=10,如果将△ABC沿AD折叠,使AC恰好落在AB边上.
(1)、在坐标系中画出;(2)、求的面积;(3)、画出关于x轴的对称图形 , 并写出点 , , 的坐标.22. 如图,△ABC的三边分别为AC=6,BC=8,AB=10,如果将△ABC沿AD折叠,使AC恰好落在AB边上. (1)、试判断△ABC的形状,并说明理由.(2)、求线段CD的长.23. 分别画出满足下列条件的点:(尺规作图,请保留作图痕迹,不写作法.作图痕迹请加粗加黑!)(1)、在边 上找一点 ,使 到 和 的距离相等;(2)、在射线 上找一点 ,使 .
(1)、试判断△ABC的形状,并说明理由.(2)、求线段CD的长.23. 分别画出满足下列条件的点:(尺规作图,请保留作图痕迹,不写作法.作图痕迹请加粗加黑!)(1)、在边 上找一点 ,使 到 和 的距离相等;(2)、在射线 上找一点 ,使 . 24. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与x轴相交于点B,与正比例函数的图象相交于点C,点C的横坐标为1.
24. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与x轴相交于点B,与正比例函数的图象相交于点C,点C的横坐标为1.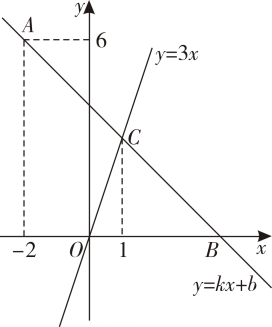 (1)、求k、b的值;(2)、请直接写出不等式的解集;(3)、若点D在y轴上,且满足 , 求点D的坐标.25. 甲、乙两车分别从B,A两地同时出发,甲车匀速前往A地,乙车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;设甲、乙两车距A地的路程为y(千米),乙车行驶的时间为x(时),y与x之间的图象如图所示.
(1)、求k、b的值;(2)、请直接写出不等式的解集;(3)、若点D在y轴上,且满足 , 求点D的坐标.25. 甲、乙两车分别从B,A两地同时出发,甲车匀速前往A地,乙车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;设甲、乙两车距A地的路程为y(千米),乙车行驶的时间为x(时),y与x之间的图象如图所示. (1)、求乙车到达B地的时间;(2)、求乙车到达B地时甲车距A地的路程;(3)、求甲车行驶途中,甲、乙两车相距40千米时,乙车行驶的时间.26. 某同学根据学习函数的经验,对函数的图像与性质进行了探究.下面是他的探究过程,请补充完整∶(1)、填表
(1)、求乙车到达B地的时间;(2)、求乙车到达B地时甲车距A地的路程;(3)、求甲车行驶途中,甲、乙两车相距40千米时,乙车行驶的时间.26. 某同学根据学习函数的经验,对函数的图像与性质进行了探究.下面是他的探究过程,请补充完整∶(1)、填表x
…
…
y
…
…
(2)、根据(1)中的结果,请在所给坐标系中画出函数的图像. (3)、结合函数图象,请写出该函数的一条性质.
(3)、结合函数图象,请写出该函数的一条性质.