北师大版数学七年级上册期末冲刺满分攻略9 有理数的乘除法

试卷更新日期：2023-12-28 类型：复习试卷

进入出卷网下载

一、选择题

1. 若干个不等于0的有理数相乘，积的符号( )

A、由因数的个数决定 B、由正因数的个数决定 C、由负因数的个数决定 D、由负因数和正因数个数的差为决定

查看试题解析
2. 下列说法正确的有（）
      $①$ 相反数是它本身的数是 $0$ ；

      $②$ 绝对值是它本身的数是正数；

      $③$ 倒数是它本身的数是 $1$ ；

      $④$ 一个有理数不是整数就是分数；

      $⑤$ 数轴上距原点 $3$ 个单位的点表示的数是 $3$ ；

      $⑥$ 绝对值相等的两数互为相反数．

A、 $2$ 个 B、 $3$ 个 C、 $4$ 个 D、 $5$ 个

查看试题解析
3. $- \frac{3}{5}$ 的倒数是（）

A、 $- \frac{3}{5}$ B、 $\frac{3}{5}$ C、 $- \frac{5}{3}$ D、 $\frac{5}{3}$

查看试题解析
4. 已知两个有理数a,b，如果ab<0,a+b<0,那么（）

A、a>0,b<0 B、a<0,b>0 C、a,b异号 D、a,b异号且负数的绝对值较大

查看试题解析
5. 绝对值不大于3的所有整数的积等于（）

A、0 B、6 C、36 D、﹣36

查看试题解析
6. 若|a|=5，|b|=3，那么a•b的值是（）

A、15 B、﹣15 C、±15 D、以上都不对

查看试题解析
7. 若x=（﹣1.125）× $\frac{4}{3}$ ÷（﹣ $\frac{3}{4}$ ）× $\frac{1}{2}$ ，则x的倒数是（）

A、1 B、﹣1 C、±1 D、2

查看试题解析
8. 一个圆柱体削去12立方分米后，正好削成一个与它等底等高的圆锥，这个圆锥体体积是（）立方分米。

A、24 B、12 C、6 D、18

查看试题解析
9. 式子4×25×（ $\frac{1}{2}$ ﹣ $\frac{3}{10}$ + $\frac{2}{5}$ ）=100（ $\frac{1}{2}$ ﹣ $\frac{3}{10}$ + $\frac{2}{5}$ ）=50﹣30+40中用的运算律是（　　）

A、乘法交换律及乘法结合律 B、乘法交换律及分配律 C、乘法结合律及分配律 D、分配律及加法结合律

查看试题解析
10. 规定：将求若干个相同的有理数（均不等于0）的除法运算叫做“除方”，如 $2 \div 2 \div 2$ ， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 等．类比有理数的乘方，我们把 $2 \div 2 \div 2$ 记作 $2^{③}$ ，读作“2的圈3次方”；把 $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 记作 $- 3^{④}$ ，读作“ $- 3$ 的圈4次方”．一般地，把 $a \div a \div ⋯ \div a \div a (a \neq 0)$ 记作 $a^{∘}$ ，读作“ $a$ 的圈 $c$ 次方”．关于“除方”，下列说法中错误的是（）．

A、任何非零数的圈2次方都等于1 B、对于任何正整数 $a$ ，都有 $a^{④} = {(\frac{1}{a})}^{2}$ C、 $3^{④} = 4^{④}$ D、负数的圈奇数次方结果是负数，负数的圈偶次方结果是正数

查看试题解析

二、填空题

11. 已知有理数a，b，c满足abc<0，a+b+c=0．则式子 $\frac{a - b - c}{| a |} + \frac{b - c - a}{| b |} + \frac{c - a - b}{| c |}$ 的值为

查看试题解析
12. 你会玩“24点”游戏吗？将下面四张扑克牌凑成24，结果是＝24，注：扑克牌下面的数是其对应的有理数．

查看试题解析
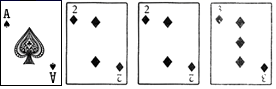13. 独立完成一项工程，甲用 $\frac{1}{2}$ 小时，乙用 $\frac{1}{3}$ 小时，的工作效率高。

查看试题解析
14. 观察下列等式： $\frac{1}{1 \times 2} = 1 - \frac{1}{2} ， \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ， \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，将以上三个等式两边分别相加得： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$ ．应用计算：
$\frac{1}{1 \times 4} + \frac{1}{4 \times 7} + \frac{1}{7 \times 10} + \frac{1}{10 \times 13} + \cdot \cdot \cdot + \frac{1}{298 \times 301} =$ ．

查看试题解析
15. 已知一组数为： $\frac{1}{3}$ ，﹣ $\frac{3}{6}$ ， $\frac{5}{11}$ ，﹣ $\frac{7}{18}$ ， $\frac{9}{27}$ …．按此规律用代数式表示第10个数为．

查看试题解析
16.
如图是一个数值转换机，若输入的x为﹣5，则输出的结果是

查看试题解析

三、解答题

17. 计算：

(1)、 $25 + (- 5) \times \frac{1}{5} + (- \frac{3}{4})$ ；

(2)、 $- 24 \times (\frac{1}{6} + \frac{3}{8} - \frac{7}{12})$ ．

查看试题解析
18. 计算：

(1)、 $(\frac{7}{8} + \frac{3}{4} - \frac{5}{6}) \div \frac{1}{24}$ ；

(2)、 $- 1^{4} + (- 2) \div (- \frac{1}{3}) - | - 9 |$

查看试题解析
19. 在数 $- 5$ ， $- 3$ ， $- 1$ ， $+ 2$ ， $+ 4$ ， $+ 6$ 中任取三个数相乘，其中最大的积是多少？最小的积是多少？

查看试题解析
20. 某市出租车的计价标准为：行驶路程不超过3千米收费10元，超过3千米的部分按每千米2.4元收费．

(1)、若某人乘坐了x（x＞3）千米，则他应支付车费元．（用含有x的代数式表示）；

(2)、一出租车公司坐落于东西向的大道边，驾驶员王师傅从公司出发，在此大道上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：千米）
第1批
第2批
第3批
第4批
+1.6
﹣9
+2.9
﹣7
①送完第4批客人后，王师傅在公司的边（填“东”或“西”），距离公司千米的位置；
②在整个过程中，王师傅共收到车费元；
③若王师傅的车平均每千米耗油0.1升，则送完第4批客人后，王师傅用了多少升油？

查看试题解析
21. 学习有理数得乘法后，老师给同学们这样一道题目：计算：49 $\frac{24}{25}$ ×（﹣5），看谁算的又快又对，有两位同学的解法如下：
小明：原式=﹣ $\frac{1249}{25}$ ×5=﹣ $\frac{1249}{5}$ =﹣249 $\frac{4}{5}$ ；
小军：原式=（49+ $\frac{24}{25}$ ）×（﹣5）=49×（﹣5）+ $\frac{24}{25}$ ×（﹣5）=﹣249 $\frac{4}{5}$ ；
（1）对于以上两种解法，你认为谁的解法较好？
（2）上面的解法对你有何启发，你认为还有更好的方法吗？如果有，请把它写出来；
（3）用你认为最合适的方法计算：19 $\frac{15}{16}$ ×（﹣8）

查看试题解析
22.
如图是小明的计算过程，请仔细阅读，并解答下列问题．
回答：（1）解题过程中有两处错误：
第1处是，错误原因是．
第2处是，错误原因是
（2）请写出正确的解答过程．

查看试题解析
23. 阅读下面的解题过程：
计算（﹣15）÷（ $\frac{1}{3}$ - $\frac{1}{2}$ ）×6
解：原式=（﹣15） $\div (- \frac{1}{6})$ ×6（第一步）
=（﹣15）÷（﹣1）（第二步）
=﹣15（第三步）
回答

(1)、上面解题过程中有两处错误，第一处是第步，错误的原因是，第二处是第步，错误的原因是

(2)、把正确的解题过程写出来

查看试题解析
24. 小华在课外书中看到这样一道题：
计算： $\frac{1}{36} \div$ （ $\frac{1}{4} + \frac{1}{12} - \frac{7}{18} - \frac{1}{36}$ ）+（ $\frac{1}{4} + \frac{1}{12} - \frac{7}{18} - \frac{1}{36}$ ） $\div \frac{1}{36}$ ．
她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，她顺利地解答了这道题

(1)、前后两部分之间存在着什么关系？

(2)、先计算哪部分比较简便？并请计算比较简便的那部分．

(3)、利用（1）中的关系，直接写出另一部分的结果．

(4)、根据以上分析，求出原式的结果．

查看试题解析

第1批	第2批	第3批	第4批
+1.6	﹣9	+2.9	﹣7