四川省德阳市中江县2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期：2023-12-28 类型：期中考试
一、选择题（本大题共12小题，共48分。在每小题列出的选项中，选出符合题目的一项）
-
1. 在下列长度的三条线段中，不能组成三角形的是（ ）A、2 cm， 3 cm. 4cm B、3 cm， 6 cm. 6cm C、2 cm， 2 cm， 6cm D、5 cm， 6 cm. 7 cm2. 下列图形中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
3. 已知△ABC中，∠A，∠B，∠C三个角的比例如下，其中能说明△ABC是直角三角形的是（ ）
A、2：3：4 B、1：2：3 C、4：3：5 D、1：2：24. 如图，△ABC≌△ADE ， 如果AB＝5cm，BC＝7cm，AC＝6cm，那么DE的长是（ ）
A、6cm B、5cm C、7cm D、无法确定5. 如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E ， ∠BAC＝60°，∠ABE＝25°，则∠DAC的大小是（ ）
A、15° B、20° C、25° D、30°6. 如图，BD＝CF ， FD⊥BC于点D ， DE⊥AB于点E ， BE＝CD ， 若∠AFD＝145°，则∠EDF的度数为（ ）
A、45° B、55° C、35° D、65°7. 如图是“一带一路”示意图，若记北京为A地，莫斯科为B地，雅典为C地，分别连接AB ， AC ， BC ， 形成一个三角形，若想建立一个货物中转仓，使其到A ， B ， C三地的距离相等，则中转仓的位置应选在（ ）
A、△ABC三条中线的交点处 B、△ABC三边的垂直平分线的交点处 C、△ABC三条角平分线的交点处 D、△ABC三条高所在直线的交点处8. 如图，△ABC中，∠B＝25°，AB的垂直平分线MN交BC于点E ， AC＝BE ， 则∠A的度数为（ ）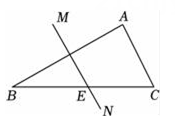
A、100° B、105° C、110° D、115°9. 如图，为了让电线杆垂直于地面，工程人员的操作方法通常是：从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC ， 当固定点B ， C到杆脚E的距离相等，且B ， E ， C在同一直线上时，电线杆DE就垂直于BC ． 工程人员这种操作方法的依据是（ ）
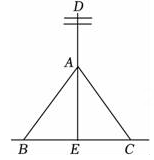A、等边对等角 B、等腰三角形“三线合一” C、垂线段最短 D、线段垂直平分线上的点到这条线段两端点的距离相等10. 有足够多的如下4种边长相等的正多边形瓷砖图案进行平面镶嵌，则不能铺满地面的是（ ）
A、①②④ B、①② C、①④ D、②③11. 如图，在△ABC中，点A的坐标为（0，1），点B的坐标为（0，4），点C的坐标为（4，3），如果要使△ABD与△ABC全等，那么点D的坐标是（ ）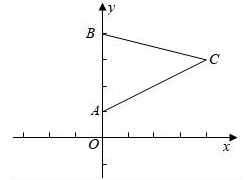
A、（﹣4，3） B、（﹣4，2） C、（4，2）或（﹣4，3） D、（4，2）或（﹣4，2）或（﹣4，3）12. 如图，四边形ABCD中，∠A＝∠C＝90°，点M、N分别是BC、AB边上的动点，∠B＝56°，当△DMN的周长最小值时，则∠MDN的度数是（ ）
A、124° B、68° C、60° D、56°二、填空题（本大题共7小题，共28分）
-
13. 点A（﹣3，2）关于y轴的对称点坐标是 ．
14. 如图，已知∠ACD＝60°，∠B＝20°，那么∠A的度数是 ．
15. 如图所示，在△ABC中，D、E分别为BC、AD的中点，且S△ABC＝4，则S阴影＝ ．
16. 如图，已知BO平分∠CBA ， CO平分∠ACB ， 且MN∥BC ， 设AB＝12，BC＝24，AC＝18，则△AMN的周长是 ．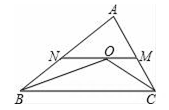
17. 若a ， b ， c分别是三角形的三边，化简|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|＝ ．18. 如图，∠AOB＝15°，M是边OA上的一个定点，且OM＝12cm ， N ， P分别是边OA、OB上的动点，则PM+PN的最小值是 ．
19. 如图BD为△ABC的角平分线，且BD＝BC ， E为BD延长线上一点，BE＝BA ， 过E作EF⊥AB于F ， 下列结论：①△ABD≌△EBC；②∠BCE+∠BDC＝180°；
③AD＝AE＝EC；④AB∥CE；
⑤BA+BC＝2BF ． 其中正确的是 ．
三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤）
-
20.(1)、已知一个多边形的每个内角都是144°，求这个多边形的内角和．(2)、生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察现实生活世界，就会有许多意想不到的收获，如图两幅图都是由同一副三角板拼凑得到的：
①如图1，求∠BCE的度数．②如图2，已知AE∥CD ， 求∠CFE的度数．
21. 如图，AD是∠BAC的平分线，DE⊥AB于E ， DF⊥AC于F ， 且DB＝DC ， 求证：BE＝CF ．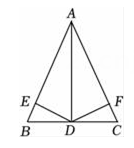
22. 在△ABC中，∠ABC＝∠C ， BD是AC边上的高线，∠ABD＝30°，求∠C的度数．23. 如图，在正方形网格上的一个△ABC ， 且每个小正方形的边长为1（其中点A ， B ， C均在网格上）．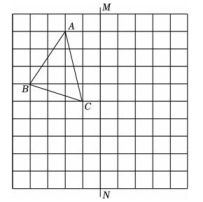
作△ABC关于直线MN的轴对称图形△A′B′C′；
在MN上画出点P ， 使得PA+PC最小；
求出△ABC的面积．
24. 已知（如图），在△ABC中，D是BC的中点，过点D的直线GF交AC于点F ， 交AC的平行线BG于点G ， DE⊥GF ， 交AB于点E ， 连接EF ．
(1)、求证：BG＝CF ．(2)、试判断BE+CF与EF的大小关系，并说明理由．25. 如图，在△ABC中，AC＝BC ， ∠ACB＝90°，点D为△ABC内一点，且BD＝AD ，
(1)、求证：CD⊥AB；(2)、∠CAD＝15°，E为AD延长线上的一点，且CE＝CA ，①求证：DE平分∠BDC；
②若点M在DE上，且DC＝DM ， 试证明ME＝BD；
③若N为直线AE上一点，且△CEN为等腰三角形，直接写出∠CNE的度数．