四川省四川大学附中2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-28 类型:期中考试
一、选择题(本大题共8个小题,每小题4分,共32分)
-
1. 下列各数中,为无理数的是( )A、 B、0 C、 D、3.52. 下列方程组是二元一次方程组的是( )A、 B、 C、 D、3. 估计 的值在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间4. 下列各组数不能作为直角三角形的三边长的是( )A、6,8,12 B、1,2, C、9,12,15 D、7,24,255. 下列图象中,是一次函数y=kx+b(其中k>0,b<0)的图象的是( )A、
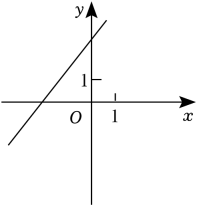 B、
B、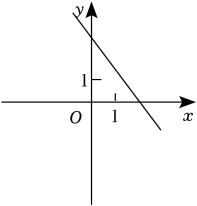 C、
C、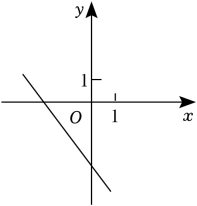 D、
D、 6. 中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
6. 中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )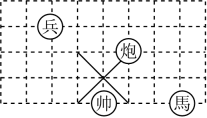 A、(﹣1,1) B、(﹣2,1) C、(﹣3,1) D、(﹣2,﹣1)7. 如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( )
A、(﹣1,1) B、(﹣2,1) C、(﹣3,1) D、(﹣2,﹣1)7. 如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是( ) A、 B、 C、 D、8. 如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH , 则线段GH的长为( )
A、 B、 C、 D、8. 如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH , 则线段GH的长为( )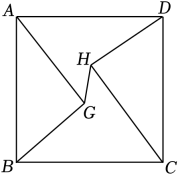 A、 B、12﹣3 C、 D、39. 计算:= .10. 平面直角坐标系中,若点A在第二象限,且到x轴的距离为3,到y轴的距离为2,则点A的坐标为 .11. 在平面直角坐标系xOy中,点P(5,﹣1)关于y轴对称的点的坐标是 .12. 如图,圆柱的高为8cm , 底面圆的周长为12cm , 一只蚂蚁从下底面的点A处沿圆柱侧面爬到上底面与点A相对的点B处觅食,则蚂蚁爬行的最短路程为 cm .
A、 B、12﹣3 C、 D、39. 计算:= .10. 平面直角坐标系中,若点A在第二象限,且到x轴的距离为3,到y轴的距离为2,则点A的坐标为 .11. 在平面直角坐标系xOy中,点P(5,﹣1)关于y轴对称的点的坐标是 .12. 如图,圆柱的高为8cm , 底面圆的周长为12cm , 一只蚂蚁从下底面的点A处沿圆柱侧面爬到上底面与点A相对的点B处觅食,则蚂蚁爬行的最短路程为 cm .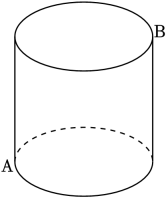 13. 如图,在△ABC中,AB=AC=5,观察尺规作图的痕迹,若BE=2,则BC的长是 .
13. 如图,在△ABC中,AB=AC=5,观察尺规作图的痕迹,若BE=2,则BC的长是 .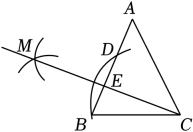
二、解答题(本大题共5个小题,共48分)
-
14.(1)、计算:(2)、解方程组:15. 已知 , , 求x2+xy+y2的值.16. 如图,平面直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.
 (1)、画△ABC关于y轴的对称图形△A1B1C1;(2)、试判断△ABC的形状,说明理由;(3)、在y轴上求作一点P , 使得PA+PB最小,并求出这个最小值.17. 如图所示,在平面直角坐标系中,过点B(3,0)的直线y1与直线OA:交于点A , ∠CBO=45°.
(1)、画△ABC关于y轴的对称图形△A1B1C1;(2)、试判断△ABC的形状,说明理由;(3)、在y轴上求作一点P , 使得PA+PB最小,并求出这个最小值.17. 如图所示,在平面直角坐标系中,过点B(3,0)的直线y1与直线OA:交于点A , ∠CBO=45°. (1)、求直线y1的表达式;(2)、在y轴上找一点P , 使SAOP=2SAOB , 求P点的坐标.18. 如图,在平面直角坐标系中,已知A(a , 0)、B(0,b)分别在坐标轴的正半轴上.
(1)、求直线y1的表达式;(2)、在y轴上找一点P , 使SAOP=2SAOB , 求P点的坐标.18. 如图,在平面直角坐标系中,已知A(a , 0)、B(0,b)分别在坐标轴的正半轴上.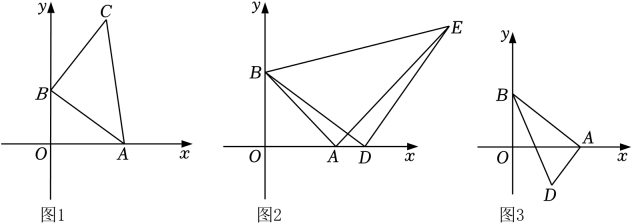 (1)、如图1.若a、b满足(a﹣4)+=0,以A为直角顶点,AB为直角边在第一象限内作等腰直角△ABC , 则点C的坐标是 ;(2)、如图2,若a=b , 点D是OA的延长线上一点,以D为直角顶点,BD为直角边在第一象限作等腰直角△BDE , 连接AE , 求证:∠ABD=AED;(3)、如图3,设AB=c , ∠ABO的平分线过点D(3,﹣3),请问a﹣b+c的值是否为定值,请说明理由.
(1)、如图1.若a、b满足(a﹣4)+=0,以A为直角顶点,AB为直角边在第一象限内作等腰直角△ABC , 则点C的坐标是 ;(2)、如图2,若a=b , 点D是OA的延长线上一点,以D为直角顶点,BD为直角边在第一象限作等腰直角△BDE , 连接AE , 求证:∠ABD=AED;(3)、如图3,设AB=c , ∠ABO的平分线过点D(3,﹣3),请问a﹣b+c的值是否为定值,请说明理由.三、填空题(本大题共5个小题,每小题4分,共20分)
-
19. 若式子有意义,则k的取值范围是 .20. 已知a2=16, =2,且ab<0,则 = .21. 已知:如图,化简代数式= .
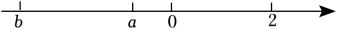 22. 对于平面直角坐标系xOy中的点P与图形M , N给出如下定义:点P到图形M上的各点的最小距离为m , 点P到图形N上各点的最小距离为n , 当m=n时,称点P为图形M与图形N的“等长点”.如:点E(﹣2,0),O(0,0),F(2,0)中,点O就是点E与点F的“等长点”,已知点A(2,0),B(2,2),C(2,﹣2),连接BC , 若点P既是点O与点A的“等长点”,也是线段OA与线段BC的“等长点”,则点P的坐标为 .23. 如图,在平面直角坐标系xOy中,点A的坐标为(0,12),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC . 若点P为OA的中点,连接PC , 则PC的长的最小值为 .
22. 对于平面直角坐标系xOy中的点P与图形M , N给出如下定义:点P到图形M上的各点的最小距离为m , 点P到图形N上各点的最小距离为n , 当m=n时,称点P为图形M与图形N的“等长点”.如:点E(﹣2,0),O(0,0),F(2,0)中,点O就是点E与点F的“等长点”,已知点A(2,0),B(2,2),C(2,﹣2),连接BC , 若点P既是点O与点A的“等长点”,也是线段OA与线段BC的“等长点”,则点P的坐标为 .23. 如图,在平面直角坐标系xOy中,点A的坐标为(0,12),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC . 若点P为OA的中点,连接PC , 则PC的长的最小值为 .
四、解答题(本大题共3个小题,共30分)
-
24. M , N两地相距160km , 甲、乙两人沿同一条路从M地到N地.OA与BC分别表示甲、乙两人离开M地的距离y(km)与时间x(h)之间的关系,根据图象解答下列问题:
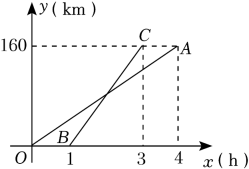 (1)、分别求出甲、乙两人离开M地的距离y与时间x之间的函数关系式;(2)、当1≤x≤3时,求两人相距20km时的时间.25. 如图,在△ABC中,已知AD是BC边上的高,过点B作BE⊥AC于点E , 交AD于点F , 且AD= , BD= , CD= .
(1)、分别求出甲、乙两人离开M地的距离y与时间x之间的函数关系式;(2)、当1≤x≤3时,求两人相距20km时的时间.25. 如图,在△ABC中,已知AD是BC边上的高,过点B作BE⊥AC于点E , 交AD于点F , 且AD= , BD= , CD= .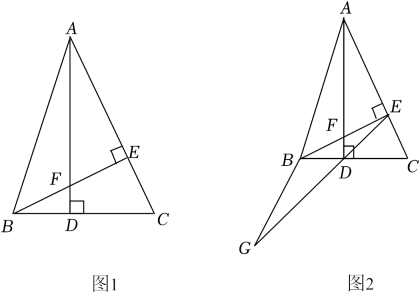 (1)、求BE的长;(2)、求证:AF=BC;(3)、如图2,在(2)的条件下,在ED的延长线上取一点G , 使BG=BE , 请猜想DG与DE的数量关系,并说明理由.26. 已知,如图1,直线AB:y=kx﹣k﹣4,分别交平面直角坐标系于A , B两点,直线CD:y=﹣2x+2与坐标轴交于C , D两点,两直线交于点E(a , ﹣a);
(1)、求BE的长;(2)、求证:AF=BC;(3)、如图2,在(2)的条件下,在ED的延长线上取一点G , 使BG=BE , 请猜想DG与DE的数量关系,并说明理由.26. 已知,如图1,直线AB:y=kx﹣k﹣4,分别交平面直角坐标系于A , B两点,直线CD:y=﹣2x+2与坐标轴交于C , D两点,两直线交于点E(a , ﹣a); (1)、求点E的坐标和k的值;(2)、如图2,点M是y轴上一动点,连接ME , 将△AEM沿ME翻折,当A点对应点刚好落在x轴上时,求ME所在直线解析式;(3)、在直线AB上是否存在点P , 使得∠ECP=45°,若存在,请求出P点坐标,若不存在请说明理由.
(1)、求点E的坐标和k的值;(2)、如图2,点M是y轴上一动点,连接ME , 将△AEM沿ME翻折,当A点对应点刚好落在x轴上时,求ME所在直线解析式;(3)、在直线AB上是否存在点P , 使得∠ECP=45°,若存在,请求出P点坐标,若不存在请说明理由.