山东省烟台市牟平区2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-28 类型:期中考试
一、选择题:(本题共10个小题,每小题3分,满分30分.每小题都给出标号A、B、C、D的四个备选答案,其中只有一个是正确的,请将正确答案用2B铅笔在答题卡上涂黑.)
-
1. 若锐角满足 , 则的度数是( )A、 B、 C、 D、2. 抛物线与直线只有一个公共点,则c的值是( )A、 B、2 C、 D、13. 按如图所示的运算程序,能使输出y值为的是( )
 A、 B、 C、 D、4. 下表中列出的是一个二次函数的自变量x与因变量y的几组对应值:
A、 B、 C、 D、4. 下表中列出的是一个二次函数的自变量x与因变量y的几组对应值:x
…
0
1
3
…
y
…
6
…
下列各选项中,正确的是( )
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于 D、当时,y的值随x值的增大而增大5. 小明骑自行车沿着斜坡向上骑行了 , 其铅直高度上升了 , 在用科学计算器求坡角α的度数时,其按键顺序是( )A、 B、
B、 C、
C、 D、
D、 6. 竖直上抛的小球的高度与运动时间的函数表达式为 , 若小球在上抛后第与第时离地面距离相等,则下列时刻中小球的高度最高的是( )A、第 B、第 C、第 D、第7. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、
6. 竖直上抛的小球的高度与运动时间的函数表达式为 , 若小球在上抛后第与第时离地面距离相等,则下列时刻中小球的高度最高的是( )A、第 B、第 C、第 D、第7. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、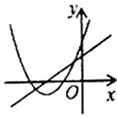 C、
C、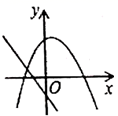 D、
D、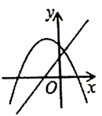 8. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )
8. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( ) A、 B、 C、 D、9. 如图,在网格正方形中,每个小正方形的边长为1,若的顶点均是格点,则的值是( )
A、 B、 C、 D、9. 如图,在网格正方形中,每个小正方形的边长为1,若的顶点均是格点,则的值是( ) A、 B、 C、0.5 D、210. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A、 B、 C、0.5 D、210. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( ) A、
A、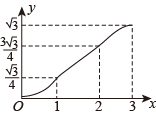 B、
B、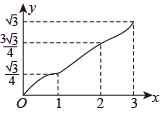 C、
C、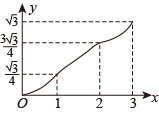 D、
D、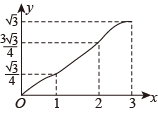
二、填空题(每题3分,共18分)
-
11. 将抛物线向左平移4个单位,再向下平移4个单位,得到抛物线的表达式是 .12. 若抛物线的部分图象如图所示,抛物线与x轴的一个交点坐标为 , 对称轴为 , 则当时,x的取值范围是 .
 13. 如图,在直角坐标系中,的顶点C与原点O重合,点A在反比例函数的图象上,点B的坐标为 , 轴,若 , 则 .
13. 如图,在直角坐标系中,的顶点C与原点O重合,点A在反比例函数的图象上,点B的坐标为 , 轴,若 , 则 . 14. 活动楼梯如图所示, , 斜坡的坡比为 , 斜坡的坡面长度为 , 则走这个活动楼梯从A点到C点上升的高度为 .
14. 活动楼梯如图所示, , 斜坡的坡比为 , 斜坡的坡面长度为 , 则走这个活动楼梯从A点到C点上升的高度为 . 15. 直角三角形纸片的两直角边长分别为6,8,现将按如图所示方式折叠,使点A与点B重合,折痕为 , 则的值为 .
15. 直角三角形纸片的两直角边长分别为6,8,现将按如图所示方式折叠,使点A与点B重合,折痕为 , 则的值为 . 16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线 . 对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则 . 其中正确结论有 . (填写序号)
16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线 . 对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则 . 其中正确结论有 . (填写序号)
三、解答题(满分72分)
-
17. 在中, , 分别是的对边.若 , 试解这个直角三角形.18. 如图1,中, , D是边上的一个动点(不与点B,C重合), , 交于点 , 交于点F . 设的长为x , 四边形的面积为y,y与x的函数图象是如图2所示的一段抛物线,其顶点P的坐标为 .
图1
 图2
图2
求:的边和的长.
19. 如图,点A在第一象限内,AB⊥x轴于点B,反比例函数 的图象分别交AO,AB于点C,D.已知点C的坐标为(2,2),BD=1. (1)、求k的值及点D的坐标.(2)、已知点P在该反比例函数图象上,且在△ABO的内部(包括边界),直接写出点P的横坐标x的取值范围.20. 如图所示,一艘渔船从海域A处到C渔港途经B岛,当它由海域A处出发时,发现它的北偏东方向有一信号塔P . 它从海域A处向正北方向航行了到达B岛,发现信号塔P在它北偏东方向,然后它由B岛向北偏东方向航行了到达C渔港.
(1)、求k的值及点D的坐标.(2)、已知点P在该反比例函数图象上,且在△ABO的内部(包括边界),直接写出点P的横坐标x的取值范围.20. 如图所示,一艘渔船从海域A处到C渔港途经B岛,当它由海域A处出发时,发现它的北偏东方向有一信号塔P . 它从海域A处向正北方向航行了到达B岛,发现信号塔P在它北偏东方向,然后它由B岛向北偏东方向航行了到达C渔港. (1)、求海域A处与信号塔P的距离;(2)、求信号塔P相对于C渔港的位置.21. 某文具店以每台30元的价格购进一批计算器,如果以每台40元出售,那么一个月内能售出300台,根据以往销售经验,销售单价每提高1元,销售量就会减少10台,设计算器的销售单价提高x元.(1)、文具店希望一个月内销售该品牌计算器能获得利润3360元,并且尽可能减少库存,问计算器的销售单价应提高多少元?(2)、当销售单价定为多少元时,该文具店一个月内销售该品牌计算器获得的利润最大?最大利润是多少元?22. 已知抛物线 .(1)、求抛物线的对称轴;(2)、把抛物线沿y轴向下平移 个单位,若抛物线的顶点落在x轴上,求a的值;(3)、设点 , 在抛物线上,若 ,求a的取值范围.23. 科技是第一生产力,无人机已广泛应用于生产和生活的各个领域,如:代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为 , 此时观测到楼底部点A处的俯角为 , 楼上点E处的俯角为 , 沿水平方向由点O飞行到达点F , 测得点E处俯角为 , 其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼与之间的距离的长(结果精确到).
(1)、求海域A处与信号塔P的距离;(2)、求信号塔P相对于C渔港的位置.21. 某文具店以每台30元的价格购进一批计算器,如果以每台40元出售,那么一个月内能售出300台,根据以往销售经验,销售单价每提高1元,销售量就会减少10台,设计算器的销售单价提高x元.(1)、文具店希望一个月内销售该品牌计算器能获得利润3360元,并且尽可能减少库存,问计算器的销售单价应提高多少元?(2)、当销售单价定为多少元时,该文具店一个月内销售该品牌计算器获得的利润最大?最大利润是多少元?22. 已知抛物线 .(1)、求抛物线的对称轴;(2)、把抛物线沿y轴向下平移 个单位,若抛物线的顶点落在x轴上,求a的值;(3)、设点 , 在抛物线上,若 ,求a的取值范围.23. 科技是第一生产力,无人机已广泛应用于生产和生活的各个领域,如:代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点O处,点O距地面的高度为 , 此时观测到楼底部点A处的俯角为 , 楼上点E处的俯角为 , 沿水平方向由点O飞行到达点F , 测得点E处俯角为 , 其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼与之间的距离的长(结果精确到).(参考数据表)
计算器按键顺序
计算结果(已精确到0.01)


2.75

0.34

1.73
 24. 如图,已知抛物线经过和两点,直线与x轴相交于点是直线上方的抛物线上的一个动点,轴交直线于点D .
24. 如图,已知抛物线经过和两点,直线与x轴相交于点是直线上方的抛物线上的一个动点,轴交直线于点D . (1)、求该抛物线的表达式;(2)、若轴交直线于点E , 求的最大值;(3)、若以为顶点的三角形与相似,请求出所有满足条件的点P , 点D的坐标.
(1)、求该抛物线的表达式;(2)、若轴交直线于点E , 求的最大值;(3)、若以为顶点的三角形与相似,请求出所有满足条件的点P , 点D的坐标.