山西省忻州地区2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-28 类型:期中考试
一、选择题(本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项符合题目要求,请将正确答案的字母标号填入下表相应的空格内。)
-
1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 戴口罩讲卫生
B、
戴口罩讲卫生
B、 勤洗手勤通风
C、
勤洗手勤通风
C、 有症状早就医
D、
有症状早就医
D、 少出门少聚集
2. 已知点与点关于原点对称,若点的坐标为 , 则点的坐标是( )A、 B、 C、 D、3. 如图,将绕点顺时针旋转得到 , 若线段 , 则的长为( )
少出门少聚集
2. 已知点与点关于原点对称,若点的坐标为 , 则点的坐标是( )A、 B、 C、 D、3. 如图,将绕点顺时针旋转得到 , 若线段 , 则的长为( ) A、3 B、4 C、5 D、64. 用配方法解方程x2+8x+7=0,则配方正确的是( )A、 B、 C、 D、5. 若关于x的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、6. 下列抛物线中,与抛物线具有相同对称轴的是( )A、 B、 C、 D、7. 下表是二次函数的几组对应值:
A、3 B、4 C、5 D、64. 用配方法解方程x2+8x+7=0,则配方正确的是( )A、 B、 C、 D、5. 若关于x的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、6. 下列抛物线中,与抛物线具有相同对称轴的是( )A、 B、 C、 D、7. 下表是二次函数的几组对应值:6.17
6.18
6.19
6.20
0.02
0.06
根据表中数据判断,方程的一个解的范围是( )
A、 B、 C、 D、8. 在长为 , 宽为的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为 , 求道路的宽度设道路的宽度为 , 则可列方程( ) A、 B、 C、 D、9. 如图,在正方形网格中,线段是线段绕某点逆时针旋转角得到的,点与点对应,则角等于( )
A、 B、 C、 D、9. 如图,在正方形网格中,线段是线段绕某点逆时针旋转角得到的,点与点对应,则角等于( ) A、45° B、60° C、90° D、120°10. 我国古代数学家研究过一元二次方程的正数解的几何解法以方程 , 即为例说明,方图注中记载的方法是:构造如图中大正方形的面积是同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此小明用此方法解关于的方程时,构造出同样的图形,已知大正方形的面积为 , 小正方形的面积为 , 则( )
A、45° B、60° C、90° D、120°10. 我国古代数学家研究过一元二次方程的正数解的几何解法以方程 , 即为例说明,方图注中记载的方法是:构造如图中大正方形的面积是同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此小明用此方法解关于的方程时,构造出同样的图形,已知大正方形的面积为 , 小正方形的面积为 , 则( )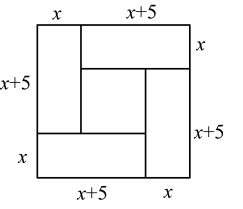 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题(每小题3分,共15分)
-
11. 若m是方程的一个根,则的值为 .12. 经文化和旅游部数据中心测算,2023年春节期间全国国内旅游出游3.08亿人次,国内多个热门景区再现游客“爆满”的景象,据统计,某景区的游客人数在春节假期第一天为4万人,第三天为5.76万人.设平均每天的增长率为x , 则可列方程为 .13. 某种型号的小型无人机着陆后滑行的距离米关于滑行的时间秒的函数解析式是 , 无人机着陆后滑行秒才能停下来.14. 如图,在中, , 将绕点按逆时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为 .
 15. 定义:在平面直角坐标系中,对于点 , 当点满足时,称点是点的“倍增点”.已知点 , 则正确的结论有 . (填写序号)
15. 定义:在平面直角坐标系中,对于点 , 当点满足时,称点是点的“倍增点”.已知点 , 则正确的结论有 . (填写序号)①点都是点的“倍增点”;
②若直线上的点A是点的“倍增点”,则点A的坐标为;
③抛物线上存在两个点是点的“倍增点”;
三、解答题(本大题共8个小题,共75分,解答应写出文字说明,证明过程或演算步骤)
-
16. 解下列一元二次方程:(1)、x2+10x+16=0;(2)、x(x+4)=8x+12.17. 下面是小颖同学解一元二次方程的过程,请认真阅读并完成相应任务.
解方程: .
解:第一步
, 第二步
, 第三步
, 第四步
或 , 第五步
. 第六步
(1)、任务一:小颖解方程的方法是(填字母);A.直接开平方法 B.因式分解法 C.配方法 D.公式法
(2)、解方程过程中,第二步变形的依据是 .(3)、请你用“公式法”解该方程.18. 如图,三个顶点坐标分别为 , , .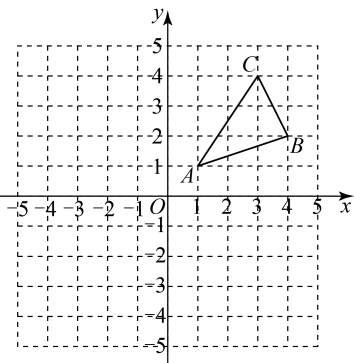 (1)、请画出关于原点O成中心对称的图形 , 并写出点 , , 的坐标;(2)、在x轴上找一点P , 使得的值最小,直接写出点P的坐标.19. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
(1)、请画出关于原点O成中心对称的图形 , 并写出点 , , 的坐标;(2)、在x轴上找一点P , 使得的值最小,直接写出点P的坐标.19. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.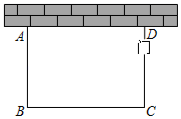 20. 如图,在中, , 将绕点逆时针旋转得到 , 其中点的对应点是 , 连接 , 当时,求旋转角的度数.
20. 如图,在中, , 将绕点逆时针旋转得到 , 其中点的对应点是 , 连接 , 当时,求旋转角的度数.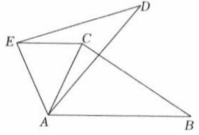 21. 在2023年1月初新冠肺炎疫情大爆发期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢?我们可以用下面的方式来解决问题.
21. 在2023年1月初新冠肺炎疫情大爆发期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢?我们可以用下面的方式来解决问题.用点、、…分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:
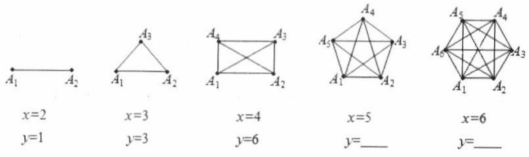 (1)、填写上图中第四个图中y的值为 , 第五个图中y的值为 .(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当时,对应的 .(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?22. 阅读与思考:
(1)、填写上图中第四个图中y的值为 , 第五个图中y的值为 .(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当时,对应的 .(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?22. 阅读与思考:根据上述材料,结合你所学的知识,完成下列问题:
(1)、材料理解:若一元二次方程的两个实数根分别为 , 则 , ;(2)、类比应用:已知一元二次方程的两个实数根分别为 , 求的值.(3)、思维拓展:已知实数满足 , 且 , 求的值.23. 综合与探究:如图,抛物线经过坐标轴上三点,直线过点和点 .
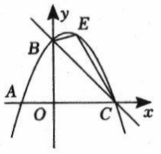 (1)、求抛物线的解析式;(2)、是直线上方抛物线上一动点,连接 , 求面积的最大值及此时点的坐标;(3)、是抛物线对称轴上的动点,在抛物线上是否存在点 , 使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条形的点坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、是直线上方抛物线上一动点,连接 , 求面积的最大值及此时点的坐标;(3)、是抛物线对称轴上的动点,在抛物线上是否存在点 , 使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条形的点坐标;若不存在,请说明理由.